Note: This html file was automatically generated from the LaTeX source.

For better formatting and quality please use the PDF version.

SPIRE Observers’ Manual _______________________________

HERSCHEL-DOC-0798, version 2.3, April 5, 2011

SPIRE Observers’ Manual

Version 2.3, April 5, 2011

This document is based on inputs from the SPIRE Consortium and the SPIRE Instrument Control Centre. Document custodian: Ivan Valtchanov, Herschel Science Centre.

Contents

1 Introduction
 1.1 The Observatory
 1.2 Purpose and Structure of Document
 1.3 Changes to Document
  1.3.1 Changes in version 2.3
  1.3.2 Changes in version 2.2
  1.3.3 Changes in version 2.1
  1.3.4 Changes in version 2.0
 1.4 Acknowledgements
 1.5 List of Acronyms
2 The SPIRE Instrument
 2.1 Instrument Overview
 2.2 Photometer design
  2.2.1 Optics and layout
  2.2.2 Beam steering mirror (BSM)
  2.2.3 Filters and passbands
  2.2.4 Photometer calibration source (PCAL)
  2.2.5 Photometer detector arrays
 2.3 Spectrometer design
  2.3.1 Fourier-Transform Spectrometer Concept and Mode of Operation
  2.3.2 Spectrometer optics and layout
  2.3.3 Spectrometer calibration source (SCAL)
  2.3.4 Filters and passbands
  2.3.5 Spectrometer detector arrays
 2.4 Common Instrument Parts
  2.4.1 Basic bolometer operations
  2.4.2 ³He cooler and thermal strap system
  2.4.3 Warm electronics
3 Observing with SPIRE
 3.1 Introduction
 3.2 SPIRE Photometer AOT
  3.2.1 Large Map
  3.2.2 Small Map
  3.2.3 Dithering of SPIRE scan maps
  3.2.4 Point Source
 3.3 SPIRE Spectrometer AOT
  3.3.1 Spectral Resolution
  3.3.2 Pointing Modes
  3.3.3 Image Sampling
  3.3.4 User input parameters for all Spectrometer AOTs.
 3.4 Using HSpot to prepare AOR
4 SPIRE in-flight performance
 4.1 Photometer performance
  4.1.1 Beam profiles
  4.1.2 Sensitivity
  4.1.3 Observing overheads
  4.1.4 Some HSpot examples
 4.2 Spectrometer
  4.2.1 Spectral range, line shape and spectral resolution
  4.2.2 Wavelength scale accuracy
  4.2.3 Beam profiles
  4.2.4 Sensitivity
  4.2.5 Some HSpot Examples
5 Flux Density Calibration
 5.1 Calibration sources and models
  5.1.1 Neptune and Uranus angular sizes and solid angles
  5.1.2 Neptune and Uranus models
  5.1.3 Mars models
  5.1.4 Asteroid models
  5.1.5 Stellar calibrators
 5.2 Photometer flux calibration scheme
  5.2.1 Photometer Relative Spectral Response Function
  5.2.2 Calibration flux densities
  5.2.3 Response of a SPIRE bolometer to incident power
  5.2.4 Conversion of RSRF-weighted flux density to monochromatic flux density
  5.2.5 Colour correction
  5.2.6 Conversion of in-beam flux density to surface brightness
  5.2.7 Photometer beam maps and areas
  5.2.8 Computed conversion factors for SPIRE
  5.2.9 Conversion from point source to extended source calibration
  5.2.10 Photometer calibration accuracy
  5.2.11 A note on point source extraction from SPIRE Level-2 maps
  5.2.12 Summary
  5.2.13 Future plans for photometer flux calibration
 5.3 Spectrometer flux calibration
  5.3.1 Spectrometer beam properties
  5.3.2 Extended sources and spectral mapping
  5.3.3 Dynamic range and interferogram clipping
  5.3.4 Bright source mode
  5.3.5 Spectrometer calibration accuracy
  5.3.6 Summary
6 SPIRE data products
Bibliography

Chapter 1
Introduction

1.1 The Observatory

The Herschel Space Observatory (Pilbratt et al., 2010) is the fourth cornerstone mission in ESA’s science programme. Herschel was successfully launched on 14^th May 2009 from Kourou, French Guiana and with its passively cooled 3.5 m diameter primary mirror is currently the largest telescope in space. Herschel is in an extended orbit around of the L2, the second Lagrangian point of the system Sun-Earth. The three on-board instruments: the Heterodyne Instrument for Far Infrared (HIFI, De Graauw et al. 2010), the Photodetector Array Camera and Spectrometer (PACS, Poglitch et al. 2010) and the Spectral and Photometric Imaging Receiver (SPIRE, Griffin et al. 2010) had their first light after the thermal stabilisation period of two months ended with the cryo-cover opening. The commissioning and performance verification phases of the instruments had started much earlier than the cryo-cover opening. These phases are very important in order to confirm that the instruments were not damaged during the launch and to validate that they will achieve their scientific objectives, namely to perform photometry and spectroscopy observations in the infrared and the far-infrared domains, from ~ 60 to ~ 672 μm. This spectral domain covers the cold and the dusty universe: from dust-enshrouded galaxies at cosmological distances down to scales of stellar formation, planetary system bodies and our own solar system objects. The operational lifetime of the observatory, as dictated by the liquid helium boil-off, is estimated to be about 3.5 years.

A high-level description of the Herschel Space Observatory is given in Pilbratt et al. (2010); more details are given in the Herschel Observers’ Manual. The first scientific results are presented in the special volume 518 of Astronomy & Astrophysics journal. Information with latest news, announcement of opportunities for observing programmes, documentation, tools etc is provided in the Herschel Science Centre web portal (http://herschel.esac.esa.int).

1.2 Purpose and Structure of Document

The purpose of this manual is to provide relevant information about the SPIRE instrument in order to help the astronomers to prepare and execute scientific observations with it.

The structure of the document is as follows: first we describe the instrument (Chapter 2), followed by the description of the available observing modes and how to use them (Chapter 3). In-flight performance of SPIRE is presented in Chapter 4. The flux calibration scheme is explained in Chapter 5. The SPIRE data products are presented in Chapter 6. The list of references is given in the last chapter.

1.3 Changes to Document

1.3.1 Changes in version 2.3

• Updated the information for the photometer beam profiles in Chapters 4 and 5.

• Updated Figure 5.5 – now the photometer RSRF is given as a function of the frequency, the wavelength scale is only given for information.

• Minor updates to the numbers in Section 5.2.9.

• Updates to the pixelisation corrections for SPIRE maps in Section 5.2.11.

1.3.2 Changes in version 2.2

• Chapter 3, added a short section about “dithering” for scan maps.

• Chapter 4

  • Updated the information for the photometer and spectrometer beam profiles.

  • Updated the sensitivity for the spectrometer, now we confirm that the noise scales down as expected for at least 100 repetitions.

  • Bright source mode for spectrometer is now taken in consideration for the spectrometer sensitivity summary.

• Chapter 5. This is a major revision of this chapter. Briefly the main updates are:

  • The flux calibration schemes for both the photometer and the spectrometer are described in detail.

  • Photometer flux calibration is now Neptune based and all the quoted numbers for different conversions are quoted for this case.

  • Photometer beam characterisation is further improved and presented as a function of map pixel size.

  • Photometer conversion from point source to extended source is explained in detail.

  • The overall photometer calibration accuracy is described.

  • Practical note on point source extraction from SPIRE level-2 maps is also given.

  • The spectrometer flux calibration scheme is presented with more details and practical considerations.

  • Updated spectrometer RSRF, based on Uranus.

  • Spectrometer beams are presented as function of frequency: both the FWHM as well as the beam solid angle for an extended emission.

  • Spectrometer bright-source mode is explained, with recommendation on when to use this mode.

• Chapter 6 is now describing only the SPIRE data products while providing references to the pipeline documentation.

• Updates to the list of references.

1.3.3 Changes in version 2.1

• A swap of the spectrometer array label for the bright source settings in Section 5.3.4. The correct numbers per array are (175, 55) Jy for (SSW, SLW).

1.3.4 Changes in version 2.0

This document is a major update of the pre-launch version 1.2 for the “Announcement of Opportunity for Key Projects”. Some of the key changes are listed below:

• Chapter 1, Introduction: minor changes to text

• Chapter 2, The SPIRE Instrument:

  • Changes to Figure 2.2 with the correct sky position of the SPIRE Spectrometer.

  • Added figures with photos of a bolometer, of the cooler, and of the detector array module.

  • Changes to the text to reflect the current in-flight numbers and conditions of the different subsystems of SPIRE and to match the published papers on SPIRE.

• Chapter 3, Observing with SPIRE. There were major changes to this chapter to reflect the in-flight observing modes.

  • The Small Map mode based on 64-point jiggle pattern was replaced by a new scan map mode with two small cross-scans.

  • Real life examples of scan map and spectral mapping coverage.

  • The information that was provided by the SPIRE instrument team for the release of each observing mode is incorporated in the relevant sections.

• Chapter 4, SPIRE in-flight performance. There were major updates to this chapter to reflect the in-flight performance of SPIRE.

• Chapter 5, Flux Density Calibration. This is a major update to the pre-flight “Calibration” chapter. It presents the calibration framework for SPIRE. Note that it is still an interim version, updates are to be released in the near future.

• Chapter 6, Pipeline and data products. This is a major update to the pre-flight chapter to reflect the actual systematic SPIRE data processing at the HSC.

• The Bibliography. Many new references were added.

1.4 Acknowledgements

This manual is provided by the Herschel Science Centre, based on inputs by the SPIRE Consortium and by the SPIRE instrument team.

1.5 List of Acronyms

Chapter 2
The SPIRE Instrument

2.1 Instrument Overview

SPIRE consists of a three-band imaging photometer and an imaging Fourier Transform Spectrometer (FTS). The photometer carries out broad-band photometry (λ∕Δλ ≈ 3) in three spectral bands centred on approximately 250, 350 and 500 μm, and the FTS uses two overlapping bands to cover 194-671 μm (447-1550 GHz).

Figure 2.1: SPIRE instrument architecture

Figure 2.1 shows a block diagram of the instrument. The SPIRE focal plane unit (FPU) is approximately 700 × 400 × 400 mm in size and is supported from the 10 K Herschel optical bench by thermally insulating mounts. It contains the optics, detector arrays (three for the photometer, and two for the spectrometer), an internal ³He cooler to provide the required detector operating temperature of ~ 0.3 K, filters, mechanisms, internal calibrators, and housekeeping thermometers. It has three temperature stages: the Herschelcryostat provides temperatures of 4.5 K and 1.7 K via high thermal conductance straps to the instrument, and the ³He cooler serves all five detector arrays.

Both the photometer and the FTS have cold pupil stops conjugate with the Herschel secondary mirror, which is the telescope system pupil, defining a 3.29 m diameter used portion of the primary. Conical feedhorns (Chattopadhaya et al., 2003) provide a roughly Gaussian illumination of the pupil, with an edge taper of around 8 dB in the case of the photometer. The same ³He cooler design (Duband et al., 1998) is used in SPIRE and in the PACS instrument (Poglitch et al., 2010). It has two heater-controlled gas gap heat switches; thus one of its main features is the absence of any moving parts. Liquid confinement in zero-g is achieved by a porous material that holds the liquid by capillary attraction. A Kevlar wire suspension system supports the cooler during launch whilst minimising the parasitic heat load. The cooler contains 6 STP litres of ³He, fits in a 200 × 100 × 100 mm envelope and has a mass of ~ 1.7 kg. Copper straps connect the 0.3-K stage to the five detector arrays, and are held rigidly at various points by Kevlar support modules (Hargrave et al., 2006). The supports at the entries to the 1.7-K boxes are also light-tight.

All five detector arrays use hexagonally close-packed feedhorn-coupled spider-web Neutron Transmutation Doped (NTD) bolometers (Turner et al., 2001). The bolometers are AC-biased with frequency adjustable between 50 and 200 Hz, avoiding 1∕f noise from the cold JFET readouts. There are three SPIRE warm electronics units: the Detector Control Unit (DCU) provides the bias and signal conditioning for the arrays and cold electronics, and demodulates and digitises the detector signals; the FPU Control Unit (FCU) controls the cooler and the mechanisms, and reads out all the FPU thermometers; and the Digital Processing Unit (DPU) runs the on-board software and interfaces with the spacecraft for commanding and telemetry.

A summary of the most important instrument characteristics is shown in Table 2.1 and the operational parts of SPIRE are presented in the subsequent sections. A more detailed description of SPIRE can be found in Griffin et al. (2010).

Table 2.1: SPIRE overall characteristics.

(a) – the unapodized spectral resolution can be low (Δσ = 0.83 cm^-1), medium (Δσ = 0.24 cm^-1) or high (Δσ = 0.04 cm^-1). See Section 4.2.1 for details.
(b) – The photometer beam FWHM are given for nominal SPIRE level-2 maps with pixel sizes (6,10,14) arcsec, see Section 5.2.7. The FTS beam size depends on wavelength. See Section 5.3.1.

SPIRE shares the Herschel focal plane with HIFI and PACS and it relative position with respect to the other two instruments is shown in Figure 2.2.

Figure 2.2: SPIRE location on sky with respect to the other two instruments sharing the Herschel focal plane. The centre of the SPIRE photometer is offset by ≈11 arcmin from the centre of the highly curved focal surface of the Herschel telescope, shown by the large shaded circle.

2.2 Photometer design

2.2.1 Optics and layout

The photometer opto-mechanical layout is shown in Figure 2.3. It is an all-reflective design (Dohlen et al. 2000) except for the dichroics used to direct the three bands onto the bolometer arrays, and the filters used to define the passbands (Ade et al. 2006). The input mirror M3, lying below the telescope focus, receives the f∕8.7 telescope beam and forms an image of the secondary at the flat beam steering mirror (BSM), M4. Mirror M5 converts the focal ratio to f∕5 and provides an intermediate focus at M6, which re-images the M4 pupil to a cold stop. The input optics are common to the photometer and spectrometer and the separate spectrometer field of view is directed to the other side of the optical bench panel by a pick-off mirror close to M6. The 4.5-K optics are mounted on the SPIRE internal optical bench. Mirrors M7, M8 and a subsequent mirror inside the 1.7-K box form a one-to-one optical relay to bring the M6 focal plane to the detectors. The 1.7-K enclosure also contains the three detector arrays and two dichroic beam splitters to direct the same field of view onto the arrays so that it can be observed simultaneously in the three bands. The images in each band are diffraction-limited over the 4’x8’ field of view.

Figure 2.3: SPIRE FPU: photometer side layout.

2.2.2 Beam steering mirror (BSM)

The BSM (M4 in Figure 2.3) is located in the optical path before any subdivision of the incident radiation into photometer and spectrometer optical chains, and is used both for photometer and FTS observations. For photometric observations the BSM is moved on a pattern around the nominal position of the source. For the FTS, the BSM is moved on a specific pattern to create intermediate or fully sampled spectral maps. It can chop up to ±2 arcmin along the long axis of the Photometer’s 4 × 8 arcmin field of view and simultaneously chop in the orthogonal direction by up to 30 arcsec. This two-axis motion allows “jiggling” of the pointing to create fully sampled image of the sky. The nominal BSM chop frequency for the photometer is 1 Hz. For scanning observations the BSM is kept at its home position.

2.2.3 Filters and passbands

The photometric passbands are defined by quasi-optical edge filters (Ade et al. 2006) located at the instrument input, at the 1.7-K cold stop, and directly in front of the detector arrays, the reflection-transmission edges of the dichroics, and the cut-off wavelengths of the feedhorn output waveguides. The filters also serve to minimise the thermal loads on the 1.7-K and 0.3-K stages. The three bands are centred at approximately 250, 350 and 500 μm and their relative spectral response curves (RSRF) are given in much more detail in Section 5.2.1 (see Figure 5.5).

2.2.4 Photometer calibration source (PCAL)

PCAL is a thermal source used to provide a repeatable signal for the bolometers (Pisano et al., 2005). It operates as an inverse bolometer: applied electrical power heats up an emitting element to a temperature of around 80 K, causing it to emit FIR radiation, which is seen by the detectors. It is not designed to provide an absolute calibration of the system; this will be done by observations of standard astronomical sources. The PCAL radiates through a 2.8 mm hole in the centre of the BSM (occupying an area contained within the region of the pupil obscured by the hole in the primary). Although optimised for the photometer detectors, it can also be viewed by the FTS arrays. PCAL is operated at regular intervals in-flight in order to check the health and the responsivity of the arrays.

2.2.5 Photometer detector arrays

The three arrays contain 139 (250 μm), 88 (350 μm) and 43 (500 μm) detectors, each with its own individual feedhorn. The feedhorn array layouts are shown schematically in Figure 2.4. The design features of the detectors and feedhorns are described in more detail in Section 2.4.1.

Figure 2.4: A schematic view of the photometer bolometer arrays, the bolometer names are also shown. Each circle represents a detector feedhorn. Those detectors centred on same sky positions are shaded in blue, the dead bolometers are shaded in grey. The 4 × 8 arcmin unvignetted field of view of each array is delineated by a red dashed rectangle. The three arrays overlap on the sky as shown in the rightmost figure, where the PLW (500 μm), PMW (350 μm) and PSW (250 μm) are depicted by red, green and blue circles respectively. The circle sizes in the rightmost figure correspond to the FWHM of the beam. The spacecraft coordinate system (Y,Z) is also shown.

The relative merits of feedhorn-coupled detectors, as used by SPIRE, and filled array detectors, which are used by PACS and some ground-based instruments such as SCUBA-2 (Audley et al., 2007) and SHARC-II (Dowell et al., 2003), are discussed in detail in Griffin et al. (2002). In the case of SPIRE, the feedhorn-coupled architecture was chosen as the best option given the achievable sensitivity, the requirements for the largest possible field of view and high stray light rejection, and limitations on the number of detectors imposed by spacecraft resource budgets. The detector feedhorns are designed for maximum aperture efficiency, requiring an entrance aperture close to 2Fλ, where λ is the wavelength and F is the final optics focal ratio. This corresponds to a beam spacing on the sky of 2λ∕D, where D is the telescope diameter. The array layouts are shown schematically in Figure 2.4, a photograph of an array module is show in Figure 2.10.

2.3 Spectrometer design

2.3.1 Fourier-Transform Spectrometer Concept and Mode of Operation

The SPIRE Fourier-Transform Spectrometer (FTS) uses the principle of interferometry: the incident radiation is separated by a beam splitter into two beams that travel different optical paths before recombining. By changing the Optical Path Difference (OPD) of the two beams with a moving mirror, an interferogram of signal versus OPD is created. This interferogram is the Fourier transform of the source spectrum. Performing the inverse Fourier transform thus produces the spectrum as a function of the frequency.

The nominal mode of operation of the FTS involves moving the scan mirror continuously (nominally at 0.5 mm s^-1, giving an optical path rate of 2 mm s^-1 due to the factor of four folding in the optics). Radiation frequencies of interest are encoded as detector output electrical frequencies in the range 3-10 Hz. For an FTS, the resolution element is given by Δσ = 1∕(2 × OPD_max), where OPD_max is the maximum optical path difference of the scan mirror. The maximum mechanical scan length is 3.5 cm, equivalent to an OPD_max of 14 cm, thus the highest resolution available is Δσ = 0.04 cm^-1, which corresponds to Δν = 1.2 GHz resolution in frequency space. The number of independent samples in the final spectrum is set by the resolution, i.e. independent points in the spectrum are separated in wavenumber space by Δσ and this is constant throughout the whole wavelength range covered by the FTS.

2.3.2 Spectrometer optics and layout

The FTS (Swinyard et al., 2003; Dohlen et al., 2000) uses two broadband intensity beam splitters in a Mach-Zehnder configuration which has spatially separated input and output ports. This configuration leads to a potential increase in efficiency from 50% to 100% in comparison with a Michelson interferometer. One input port views a 2.6 arcmin diameter field of view on the sky and the other an on-board reference source (SCAL). Two bolometer arrays at the output ports cover overlapping bands of 194-313 μm (SSW) and 303-671 μm (SLW). As with any FTS, each scan of the moving mirror produces an interferogram in which the spectrum of the entire band is encoded with the spectral resolution corresponding to the maximum mirror travel.

The FTS focal plane layout is shown in Figure 2.5. A single back-to-back scanning roof-top mirror serves both interferometer arms. It has a frictionless mechanism using double parallelogram linkage and flex pivots, and a Moiré fringe sensing system. A filtering scheme similar to the one used in the photometer restricts the passbands of the detector arrays at the two ports, defining the two overlapping FTS bands.

Figure 2.5: SPIRE FPU: spectrometer side layout.

2.3.3 Spectrometer calibration source (SCAL)

A thermal source, the Spectrometer Calibrator (SCAL, Hargrave et al. 2006), is available as an input to the second FTS port to allow the background power from the telescope to be nulled, thus reducing the dynamic range (because the central maximum of the interferogram is proportional to the difference of the power from the two input ports). SCAL is located at the pupil image at the second input port to the FTS, and has two sources which can be used to simulate different possible emissivities of the telescope: 2% and 4%.

The in-flight FTS calibration measurements of Vesta, Neptune and Uranus with SCAL off showed that the signal at the peak of the interferogram is not saturated or at most only a few samples are saturated, which means that SCAL is not required to reduce the dynamic range. This is a consequence of the lower emissivity of the telescope and the low straylight in comparison with the models available during the design of the FTS. On the other hand, using the SCAL adds photon noise to the measurements and it was decided that it will not be used during routine science observations. An additional benefit from having the SCAL off is that it, and the rest of the instrument, are at a temperature between 4.5-5 K and the thermal emission from these components is limited to the low frequencies (low wavenumbers, long wavelength) only detectable in the SLW band.

2.3.4 Filters and passbands

The spectral passbands are defined by a sequence of metal mesh filters at various locations and by the waveguide cut-offs and provide two overlapping bands of 194-313 μm (SSW) and 303-671 μm (SLW). The spectrometer filters transmissions are shown in Figure 2.6. Note that the filter transmissions are only provided here for information, they are not actually used in the spectrometer processing or calibration. More useful information provide relative spectral response curves (RSRF) presented in greater details in Section 5.3.

Figure 2.6: SPIRE Spectrometer filter transmissions for the central detectors.

2.3.5 Spectrometer detector arrays

The two spectrometer arrays contain 19 (SLW) and 37 (SSW) hexagonally packed detectors, each with its own individual feedhorn, see Figure 2.7. The array modules are similar to those used for the photometer, with an identical interface to the 1.7-K enclosure. The feedhorn and detector cavity designs are optimised to provide good sensitivity across the whole wavelength range of the FTS. The SSW feedhorns are sized to give 2Fλ pixels at 225 μm and the SLW horns are 2Fλ at 389 μm. This arrangement has the advantage that there are many co-aligned pixels in the combined field of view. The SSW beams on the sky are 33 arcsec apart, and the SLW beams are separated by 51 arcsec. Figure 2.7 shows also the overlap of the two arrays on the sky with circles representing the FWHM of the response of each pixel. The unvignetted footprint on the arrays (diameter 2 arcmin) contains 7 pixels for SLW and 19 pixels for SSW, outside this circle the data is not-well calibrated. The design features of the detectors and feedhorns are described in more detail in Section 2.4.1.

Figure 2.7: A schematic view of the FTS bolometer arrays, the bolometer names are also shown. Each circle represents a detector feedhorn. Those detectors centred on same sky positions are shaded in blue, the dead bolometers are shaded in grey. The 2.6 arcmin unvignetted field of view of each array is delineated by a red dashed circle. The two arrays overlap on the sky as shown in the rightmost figure, where the SLW and SSW are depicted by red and blue circles respectively. The bold red circle delineates the 2 arcmin unvignetted field of view for FTS observations. The circle sizes in the rightmost figure correspond to the FWHM of the beam. The spacecraft coordinate system (Y,Z) is also shown.

2.4 Common Instrument Parts

2.4.1 Basic bolometer operations

The SPIRE detectors for both the photometer and the spectrometer are semiconductor bolometers. The general theory of bolometer operation is described in Mather (1982) and Sudiwala et al. (2002), and details of the SPIRE bolometers are given in Turner et al. (2001); Rownd et al. (2003) and Chattopadhaya et al. (2003).

Figure 2.8: Basic principles of bolometer operation.

The basic features of a bolometer and the principles of bolometer operation are outlined here, and are illustrated in Figure 2.8. The radiant power to be detected is incident on an absorber of heat capacity C. Heat is allowed to flow from the absorber to a heat sink at a fixed temperature T₀ by a thermal conductance, G (the higher G, the more rapidly the heat leaks away). A thermometer is attached to the absorber, to sense its temperature. A bias current, I, is passed throughout the thermometer, and the corresponding voltage, V , is measured. The bias current dissipates electrical power, which heats the bolometer to a temperature, T, slightly higher than T₀. With a certain level of absorbed radiant power, Q, the absorber will be at some temperature T, dictated by the sum of the radiant and electrical power dissipation. If Q changes, the absorber temperature will change accordingly, leading to a corresponding change in resistance and hence in output voltage.

In the case of the SPIRE detectors, the absorber is a spider-web mesh composed of silicon nitride with a thin resistive metal coating to absorb and thermalise the incident radiation. The thermometers are crystals of Neutron Transmutation Doped (NTD) germanium, which has very high temperature coefficient of resistance. A magnified view of an actual SPIRE bolometer is shown in Figure 2.9.

The main performance parameters for bolometric detectors are the responsivity (dV∕dQ), the noise-equivalent power (NEP) and the time constant (τ ~ C∕G). In order to achieve high sensitivity (low NEP) and good speed of response, operation at low temperature is needed. The photon noise level, arising from unavoidable statistical fluctuations in the amount of background radiation incident on the detector, dictates the required sensitivity. In the case of SPIRE, this radiation is due to thermal emission from the telescope, and results in a photon noise limited NEP on the order of a few ×10^-17 W Hz^-1∕2. The bolometers are designed to have an overall NEP dominated by this contribution. To achieve this, the operating temperature for the SPIRE arrays must be of the order of 300 mK.

Figure 2.9: Magnified view of a SPIRE bolometer, the thermometer size is 10x100x300 μm.

The operating resistance of the SPIRE bolometers is typically a few MΩ. The outputs are fed to JFETs located as close as possible to the detectors, in order to convert the high-impedance signals to a much lower impedance output capable of being connected to the next stage of amplification by a long cryoharness.

The thermometers are biased by an AC current, at a frequency in the 100-Hz region. This allows the signals to be read out at this frequency, which is higher than the 1∕f knee frequency of the JFETs, so that the 1∕f noise performance of the system is limited by the detectors themselves, and corresponds to a knee frequency of around 100 mHz.

Figure 2.10: Photograph of a SPIRE detector array module.

The detailed design of the bolometer arrays must be tailored to the background power that they will experience in flight, and to the required speed of response. The individual SPIRE photometer and spectrometer arrays have been optimised accordingly.

The bolometers are coupled to the telescope beam by conical feedhorns located directly in front of the detectors on the ³He stage. Short waveguide sections at the feedhorn exit apertures lead into the detector cavities. The feedhorn entrance aperture diameter is set at 2Fλ, where λ is the design wavelength and F is the final optics focal ratio. This provides the maximum aperture efficiency and thus the best possible point source sensitivity (Griffin et al., 2002). The feedhorns are hexagonally close-packed, as shown in the photograph in Figure 2.10 and schematically in Figure 2.4 and Figure 2.7, in order to achieve the highest packing density possible. A centre-centre distance of 2Fλ in the focal plane corresponds to a beam separation on the sky of 2λ∕D, where D is the telescope diameter. This is approximately twice the beam FWHM, so that the array does not produce an instantaneously fully sampled image. A suitable scanning or multiple-pointing (“jiggling”) scheme is therefore needed for imaging observations.

2.4.2 ³He cooler and thermal strap system

The same ³He cooler design (Duband et al., 1998), shown in Figure 2.11, is used for both SPIRE and PACS instruments. This type of refrigerator consists of a sorption pump and an evaporator and uses porous material which absorbs or releases gas depending on its temperature. The refrigerator contains 6 litres of liquid ³He. At the beginning of the cold phase, all of this is contained in liquid form in the evaporator. The pump is cooled to ~ 2 K, and cryo-pumps the ³He gas, lowering its vapour pressure and so reducing the liquid temperature. The slow evaporation of the ³He provides a very stable thermal environment at 300 mK for around 48 hours under constant heat load in normal observing and operational circumstances.

Figure 2.11: SPIRE cooler

Once most of the helium is evaporated and contained in the pump then the refrigerator must be recycled. This is carried out by heating of the sorption pump to ~ 40 K in order to expel the absorbed gas. The gas re-condenses as liquid at ~ 2 K in the evaporator. Once all of the ³He has been recondensed, the pump is cooled down again and starts to cryo-pump the liquid, bringing the temperature down to 0.3 K once again. This recycling takes about 2.5 hours and is usually performed during the daily telecommunications period (DTCP). Gas gap heat switches control the cooler and there are no moving parts. The confinement of the ³He in the evaporator at zero-g is achieved by a porous material that holds the liquid by capillary attraction. A Kevlar wire suspension supports the cooler during launch whilst minimising the parasitic heat load. Copper straps connect the cooler 0.3 K stage to the five detector arrays, and are held rigidly at various points by Kevlar support modules. The supports at the entries to the spectrometer and photometer 1.7 K boxes are also designed to be light-tight.

2.4.3 Warm electronics

There are three SPIRE warm electronics units. The Detector Control Unit (DCU) provides the bias and signal conditioning for the arrays and cold electronics, and demodulates and digitises the detector signals. The FPU Control Unit (FCU) controls the ³He cooler, the Beam Steering Mechanism and the FTS scan mirror, and also reads out all the FPU thermometers. The Digital Processing Unit (DPU) runs the on-board software interfaces with the spacecraft for commanding and telemetry. The 130 kbs available data rate allows all photometer or spectrometer detectors to be sampled and the data transmitted to the ground with no on-board processing.

Chapter 3
Observing with SPIRE

3.1 Introduction

An observation with SPIRE (or any of the Herschel instruments) is performed following an Astronomical Observation Request (AOR) made by the observer. The AOR is constructed by the observer by filling in the so called Astronomical Observation Template (AOT) in the Herschel Observation Planning Tool, HSpot. Each template contains options to be selected and parameters to be filled in, such as target name and coordinates, observing mode etc. How to do this is explained in details in the HSpot user’s manual while in the relevant sections in this chapter we explain the AOT user inputs.

Once the astronomer has made the selections and filled in the parameters on the template, the template becomes a request for a particular observation, i.e. an AOR. If the observation request is accepted via the normal proposal-evaluation-time allocation process then the AOR content is subsequently translated into instrument and telescope/spacecraft commands, which are up-linked to the observatory for the observation to be executed.

There are three Astronomical Observation Templates available for SPIRE: one for doing photometry just using the SPIRE Photometer, one to do photometry in parallel with PACS (see The Parallel Mode Observers’ Manual for details on observing with this mode) and one using the Spectrometer to do imaging spectroscopy: this covers all spatial resolutions and high, medium or low spectral resolution.

Building Blocks: Observations are made up of logical operations, such as configuring the instrument, initialisation and science data taking operations. These logical operations are referred to as building blocks. The latter operations are usually repeated several times in order to build up S/N and/or to map an area of sky. Pipeline data reduction modules work on building blocks (see Chapter 6).

Configuring and initialising the instrument: It is important to note that the configuration of the instrument, i.e. the bolometer parameters, like setting the bias, the science data and housekeeping data rates etc., are only set once at the beginning of the observations with this sub-instrument. There are however detector settings that are set up at the beginning of each observation, like the bolometer A/C offsets. It is not possible to change the settings dynamically throughout an observation and this may have implications (mainly signal clipping or signal saturation) for observations of very bright sources with strong surface brightness gradients.

PCAL: During SPIRE observations, the photometer calibration source, PCAL, is operated at intervals to track any responsivity drifts. Originally it was planned to use PCAL every 45 minutes, but in-flight conditions have shown excellent stability and following performance verification phase a new scheme has been adopted where PCAL is only used once at the end of an observation. This adds approximately 20 seconds to each photometer observation. For the spectrometer this can take a few seconds longer as the SMEC must be reset to its home position.

3.2 SPIRE Photometer AOT

This SPIRE observing template uses the SPIRE photometer (Section 2.2) to make simultaneous photometric observations in the three photometer bands (250, 350 and 500 μm). It can be used with three different observing modes:

• Large areas maps: This mode is for covering large areas of sky or extended sources larger than 5 arcmin diameter. The map is made by scanning the telescope.

• Small area maps: This is for sources or areas with diameters smaller than 5 arcmin. The map is made by two short cross-scans with the telescope.

• Point source photometry: This mode is for photometric observations of isolated point sources. It uses chopping, jiggling and nodding, observing the source at all times.

3.2.1 Large Map

Description

The build up of a map is achieved by scanning the telescope at a given scan speed (Nominal at 30′′/s or Fast at 60′′/s) along lines. This is shown in Figure 3.1.

Figure 3.1: Large Map build up with telescope scanning, showing the scan angle, the scan legs and the guaranteed map area.

As the SPIRE arrays are not fully filled, the telescope scans are carried out at an angle of ±42.4 deg with respect to the Z-axis of the arrays and the scan lines are separated by 348 arcsec to provide overlap and good coverage for fully sampled maps in the three bands. This is shown schematically in Figure 3.1. One scan line corresponds to one building block.

Cross-linked scanning (or cross scanning) is achieved by scanning at +42.4 deg (Scan A angle) and then at -42.4 deg (Scan B angle), see Figure 3.3. The cross-scan at Scan A and B is the default Large Map scan angle option in HSpot. This ensures improved coverage of the mapped region. Although the 1∕f knee for SPIRE is below 0.1 Hz (Griffin et al., 2010), the cross-scanning also help to reduce the effect of the 1∕f noise when making maps with maximum likelihood map makers like MADMAP(Cantalupo et al., 2010). Note that the 1∕f noise will be less significant at the faster scan speed.

Real coverage maps for the cross scanning and single direction scanning for the different SPIRE bands can be found in Section 3.2.1.

Figure 3.2: Large Map coverage showing the scan direction with respect to the SPIRE arrays, the scan leg separation step and the uniform sensitivity coverage region. The darker the shading the deeper the coverage.

Figure 3.3: Large Map scan angles.

When 1∕f noise is not a concern, the observer can choose either one of the two possible scan angles, A or B. The two are equivalent in terms of observation time estimation, overheads, sensitivities, but one may be favourable, especially when the orientation of the arrays of the sky does not vary much (due to either being near the ecliptic or to having a constrained observation, see below).

To build up integration time, the map is repeated an appropriate number of times. For a single scan angle, the area is covered only once. For cross-linked scanning, one repetition covers the area twice, once in each direction. Hence cross-linked scanning takes about twice as long and gives better sensitivity (see e.g. Figure 3.6).

Cross-linked scanning is limited to an area of just under 4 degrees square, whereas single direction scans can be up to nearly 20 degrees in the scan direction and just under 4 degrees in the other direction. Hence with a single scan direction it is possible to make very long rectangular maps. Note that cross-scan observations for highly rectangular areas are less efficient as many shorter scans are needed in one of the directions.

The dimensions of the area to be covered are used to automatically set the length and the number of the scan legs. The scan length is set such that the area requested has good coverage throughout the map and that the whole array passes over all of the requested area with the correct speed. The number of scan legs is calculated to ensure that the total area requested by the user is observed without edge effects (a slightly larger area will be covered due to the discrete nature of the scans). Hence the actual area observed will always be bigger than what was requested.

The area is by default centred on the target coordinates; however this can be modified using map centre offsets (given in array coordinates). This can be useful when one wants to do dithering or to observe the core of an object plus part of its surroundings, but does not mind in which direction from the core the surrounding area is observed.

The scans are carried out at a specific angle to the arrays, and the orientation of the arrays on the sky changes as Herschel moves in its orbit. The actual coverage of the map will rotate about the target coordinates depending on the exact epoch at which the data are taken (except for sources near the ecliptic plane where the orientation of the array on the sky is fixed: see the Herschel Observers’ Manual). This is shown in Figure 3.1.

To guarantee that the piece of sky you want to observe is included in the map, you can oversize the area to ensure that the area of interest is included no matter what the date of observation. This works well for square-like fields, but for highly elongated fields the oversizing factor would be large. To reduce the amount of oversizing needed for the map you can use the Map Orientation “Array with Sky Constraint” setting to enter a pair of angles A1 and A2, which should be given in degrees East of North. The orientation of the map on the sky, with respect to the middle scan leg, will be restricted within the angles given. This reduces the oversizing, but the number of days on which the observation can be scheduled is also reduced.

Note also that, as explained in Herschel Observers’ Manual, parts of the sky do not change their orientation with respect to the array and therefore it is not possible to set the orientation of the map in certain directions (the ecliptic) as the array has always the same orienatation. The constraints on when the observation can be performed make scheduling and the use of Herschel less efficient, hence the observer will be charged 10 minutes observatory overheads (instead of 3 minutes) to compensate (see the Herschel Observers’ Manual).

Warning: Setting a Map Orientation constraint means that your observation can only be performed during certain periods, and the number of days that your observation can be scheduled will be reduced from the number of days that the target is actually visible, because it is a constraint on the observation, not the target itself. In setting a constraint you will need to check that it is still possible to make your observation.

-

User inputs

The user inputs in HSpot are shown Figure 3.4 and summarised below:

Repetition factor:
The number of times the full map area is repeated to achieve the required sensitivity. For cross-linked maps (Scan Angles A and B), there are two coverages per repetition, one in each direction. For single scan direction observations (Scan Angle A or Scan Angle B), one coverage is performed per repetition.

Length:
This is the scan length of the map (in arcmin). It corresponds to the length in the first scan direction.

Height:
This is the size of the map (in arcmin) in the other dimension.

Scan speed:
This can be set as Nominal, 30′′/s (the default value) or Fast, 60′′/s.

Scan direction:
The choices are Scan Angles A and B (the default option, giving a cross-linked map), Scan Angle A, or Scan Angle B.

Map centre offset Y, Z:
This is the offset (in arcmin) of the map centre from the input target coordinates along the Y or Z axes of the arrays. The minimum offset is ±0.1 arcmin and the maximum allowed is ±300 arcmin.

Figure 3.4: Large Map parameters in HSpot

Map Orientation:
This can be set at either Array or Array with Sky Constraint. The latter option can be entered by selecting a range of map orientation angles for the observation to take place. The orientation angle is measured from the equatorial coordinate system North to the direction of the middle scan leg direction, positive East of North, following the Position Angle convention. The orientation constraint means a scheduling constraint and should therefore be used only if necessary.

Angle from/to:
In the case when Array with Sky Constraint is selected, the pair of angles (in degrees) between which the middle scan leg can lie along.

Source Flux Estimates (optional):
An estimated source flux density (in mJy) and/or an estimated extended source surface brightness (MJy/sr) may be entered for any of the three photometer bands, in which case the expected S/N for that band will be reported back in the Time Estimation. The sensitivity results assume that a point source has zero background and that an extended source is not associated with any point sources. The point source flux density and the extended source surface brightness are treated independently by the sensitivity calculations. If no value is given for a band, the corresponding S/N is not reported back. The time estimation will return the corresponding S/N, as well as the original values entered, if applicable.
Bright Source Setting (optional): this mode has to be selected if the expected flux of the source is above 200 Jy (see Section 4.1.2).

The maximum allowed Length and the Height for a cross-linked large maps (Scan Angles A and B) are 226 arcmin for both directions. For scans in either Scan Angle A or Scan Angle B, the maximum Length is 1186 arcmin and the maximum Height is 240 arcmin.

-

Coverage Maps

Coverage maps for cross scanning and for single direction scanning for each of the three bands are shown in Figure 3.5. These were taken from standard pipeline processing of real observations with SPIRE. Note that the coverage maps are given as number of bolometer hits per sky pixel. The standard sky pixels for the SPIRE Photometer maps are (6, 10, 14) arcsec (see Section 4.1.1).

Figure 3.5: Example coverage maps for Large Map mode for the three photometer arrays, PSW (left), PMW (centre) and PLW (right). The top row is for a single scan A observation. The bottom row is for a cross-linked scan of 30 × 30 arcmin field, the white circle is the user requested area. The pixel size is (6,10,14) arcsec for (PSW, PMW, PLW) and the colour code represents the number of bolometer hits in each sky pixel.

Time estimation and sensitivity

The estimated time to perform a single scan and cross-linked scans for one square degree field (60 × 60 arcmin) and one repetitions are given in the HSpot screenshots in Figure 3.6.

Figure 3.6: Large Map time estimation and sensitivity for a filed of 60×60 and one repetition for a cross-linked (scan A and B, left) and single scan direction (right).

The sensitivity estimates are subject to caveats concerning the flux density calibration (see Section 5.2). The reported 1-σ noise level does not include the confusion noise, which ultimately limits the sensitivity (see Herschel Confusion Noise Estimator for more details). It is important to keep in mind that the galactic confusion noise can vary considerably over the sky.

When to use this mode

Large map mode is used to cover large fields, larger than 5 arcmin diameter, in the three SPIRE photometer bands. Note that the mode can still be used even for input height and width of 5 arcmin, however the efficiency is low and the map size will be much larger than the requested 5x5 arcmin field.

The coverage map for a single scan observation is inhomogeneous due to missing or noisy bolometers (see Figure 3.5). Even though the 1∕f noise is not a big effect even for single scan maps our advice is to use cross-linked maps when a better flux reconstruction is needed (i.e. deep fields, faint targets, etc).

3.2.2 Small Map

Description

The SPIRE Small Map mode is designed for observers who want a fully sampled map for a small < 4 arcmin area of sky. The original SPIRE Small Map mode was initially a 64-point Jiggle Map. However, after analysis and investigation this has been replaced by a 1 × 1 small scan map using nearly orthogonal (at 84.8 deg) scan paths.

The Small Scan Map mode is defined as follows;

• 1x1 nearly orthogonal scan paths.

• Scan Angles are fixed at ±42.4 degrees with respect to the Spacecraft Z-axis.

• Fixed scan path with guaranteed coverage of 5 arcmin diameter circle.

• Fixed scan speed = 30′′/s.

• Calibration PCAL flash made only at end of Observation.

• Map offsets available.

• Otherwise identical to the SPIRE Large Scan Map mode.

User inputs

The user inputs in HSpot are shown in Figure 3.7, left and described below.

Figure 3.7: User inputs in HSpot for Small Map AOT (left) and Small Map mode time estimation, sensitivity estimate for one repetition of the map.

Repetition factor:
The number of repeats of the 1x1 scan pattern.

Map Centre Offset Y and Z:
This is the offset (in arcmin) of the map centre from the input target coordinates along the Y or Z axis of the arrays. The minimum offset is ±0.1 arcmin and the maximum allowed is ±300 arcmin.

Source Flux Estimates (optional):
An estimated source flux density (in mJy) may be entered for a band, in which case the expected S/N for that band will be reported back in the Time Estimation. The sensitivity results assume that a point source has zero background. If no value is given for a band, the corresponding S/N is not reported back.

Bright Source Setting (optional):
this mode has to be selected if the expected flux of the source is above 200 Jy (see Section 4.1.2).

Time estimation and sensitivity

The time estimation and sensitivities are shown in Figure 3.7, right. The sensitivity estimates and the caveats are the same as the Large Map mode.

Coverage maps

The coverage maps at 250, 350 and 500 μm from a real observation are shown in Figure 3.8. For a given observation the area covered by both scan legs defines a central square of side 5 arcmin although the length of the two orthogonal scan paths are somewhat longer than this. In practice, due to the position of the arrays on the sky at the time of a given observation, the guaranteed area for scientific use is a circle of diameter 5 arcmin.

Figure 3.8: Example coverage maps for Small Map mode for the three photometer arrays, PSW (left), PMW (centre) and PLW (right), taken from a real observaiton. The white circle is with 5 arcmin diameter. The pixel size is (6,10,14) arcsec for (PSW, PMW, PLW) and the colour code represents the number of bolometer hits in each sky pixel.

When to use this mode

This mode has the same sensitivity as the Large Map mode but for small areas it uses less time.

3.2.3 Dithering of SPIRE scan maps

By default, SPIRE scan maps provide excellent spatial sampling of the region being surveyed. For repeated observations of the same field the user has the option of specifying multiple AORs (rather than a single multiple-repetition AOR), offset from each other by a small distance (“dithering”), to produce a more uniform coverage over the map. Note that it has not yet been demonstrated that dithering produces any noticeable improvement in data quality, and there is an additional overhead cost of at least 180 s involved in its implementation1 .

Figure 3.9: Offsets for the 19-point dithering pattern, with the target position at (0, 0). The drawing shows the PSW array, with the holes for the currently dead PSW bolometers.

Here we present one example of how dithering can be implemented should the observer wish to do so.2 The method uses the option in HSpot to enter map centre offsets (see Figures 3.4 and 3.7). These offsets (φ_Y, φ_Z) should be in arcmin in the telescope coordinate system (Y,Z). Figure 3.9 shows an example of 19-point dithering: the AOR centres are distributed around the edges of a rectangle in the Y and Z axes, in order to give more uniform sampling with respect to the A and B scan directions, spread evenly across the separation between two adjacent scan legs (348 arcsec for SPIRE scan maps). This spacing was chosen because the main source of non-uniformity in the sampling comes from the overlap between adjacent scan legs. Using the (Y,Z) reference system ensures that the relative configuration of the dithering pattern with respect to the scan axes will remain the same regardless of when the observation will be executed, i.e. the whole plane of Figure 3.9 will rotate but the configuration will remain the same. For this particular example of 19-point dithering the offsets are:

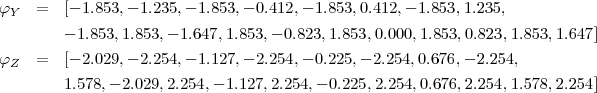
To use this scheme the observer needs to create 19 SPIRE map AORs (Large or Small Maps), each one with the corresponding pair of Y,Z offsets: (-1.853,-2.09), (-1.235, -2.254) …(1.647,2.254). In principle, each AOR comes with an observatory overhead of 180 s, but concatenating the 19 AORs will only incur an overhead of 180 s only for the first AOR (see the HSpot help, Section 16.4). Note that it is always a good idea to check the AOR overlays in HSpot in order to ensure that the dithering pattern is set up correctly.

Figure 3.10 illustrates the achievement of more uniform coverage through this technique. It should be noted that the coverage in a standard SPIRE map is already comfortably oversampled with respect to the Nyquist criterion.

Figure 3.10: Coverage maps, convolved with the beam, for no dithering (top) and 19-point dithering (bottom), for 250 μm (left), 350 μm (middle) and 500 μm (right). The white square shows a 30 × 30 arcmin field. Note that the colour scales are different for the top and bottom panels.

Observers contemplating using dithering are advised to seek guidance from the Herschel Science Centre.3

3.2.4 Point Source

Description

A mini-map is made around the nominal position to make sure that the source signal and position can be estimated. This mini-map is made by moving the BSM around to make the map as shown in Figure 3.11 for one detector. The 7-point map is made by observing the central position and then moving the BSM to observe six symmetrically arranged positions (jiggle), offset from the central position by a fixed angle (nominally 6 arcsec), and then returning to the central point once more (note that the 7 in 7-point refers to the number of different positions). At each of these positions chopping is performed between sets of co-aligned detectors (Figure 3.11, right) to provide spatial modulation and coverage in all three wavelength bands.

Figure 3.11: Left: the 7-point hexagonal jiggle pattern. Note that the central point is revisited at the end. The seven points are used to fit the 2-D beam as shown in the drawing. Right: the image shows the central co-aligned pixels as they appear on the sky. The circles numbered 1 and 2 show the detectors on which a point source is viewed via the chopping and nodding which is described in detail in the text. The angular positions of detectors are also shown.

The chop direction is fixed along the long axis of the array (Y), and the chop throw is 126 arcsec. The nominal chop frequency is 1 Hz. Sixteen chop cycles are performed at each jiggle position. Nodding, once every 64 seconds, is performed along the Y axis to remove differences in the background seen by the two detectors.

Figure 3.11, right, shows the central row of co-aligned pixels. At the first nod position (nod A at 0,0) the source is repositioned with the BSM on detector 1 and the chopping is performed between 1 and 2. Then the telescope nods at +126 arcsec (as shown in the figure), this is nod B, and the target is repositioned with the BSM on detector 2. The chopping is between 2 and 3. Note that in this scheme detector 4 is not used. This is one AB cycle. The standard Point source photometry observation uses ABBA cycle, i.e. we repeat in reverse the same scheme. To acquire further integration time, the ABBA nod pattern is repeated an appropriate number of times: ABBA ABBA etc.

The chop and nod axis is the same and is parallel to the long axis of the array to allow switching between co-aligned pixels. As Herschel moves in its orbit, the orientation of the array on the sky changes. To avoid chopping nearby bright sources onto the arrays (see e.g. Figure 3.13), pairs of angles can be defined (up to three pairs are allowed) which will prevent the observation being made when the long axis of the arrays lies between the specified angles. Note that both the specified angle range and its equivalent on the other side of the map (± 180 degrees) are avoided.

Setting a chop avoidance criterion means that an observation will not be possible during certain periods, and the number of days on which the observation can be made will be reduced from the number of days that the target is actually visible (visibility in HSpot does not take into account the constraint). In setting a constraint you will therefore need to check that it is still possible to make your observation and that you have not blocked out all dates. Note also that, as explained in the Herschel Observers’ Manual, parts of the sky near the ecliptic plane do not change their orientation with respect to the array and therefore it is not possible to avoid chopping in certain directions.

Figure 3.12: HSpot user inputs for Point Source mode (left) and the HSpot time estimation for Point Source mode (right).

A practical tip is to transform the pair of chop avoidance angles (A1, A2) to pairs of position angles of the Herschel focal plane. Then, with the help of the HSpot target visibility tool, the days when the focal plane position angle does not fall between the derived angles can be identified. As the chopping is on the Y-axis then the pair of chop avoidance angles (A1,A2) corresponds to two pairs of Herschel focal plane position angles (PA1,PA2) = (A1, A2) ± 90, which have to be avoided.

Warning: The constraints on when the observation can be performed make scheduling and the use of Herschel less efficient. The observer will be charged extra 10 minutes in overheads (rather than the usual 3) to compensate.

-

Table 3.1: The basic parameters for the Point Source mode.

User Inputs

The user input in HSpot are shown in Figure 3.12 and explained below.

Repetition factor:
The number of times the nod cycle ABBA is repeated to achieve the required sensitivity.

Number of chop avoidances:
An integer between 0 and 3.

Chopping Avoidance Angles From/To:
To be used when number of chop avoidances is greater than zero. A From/To pair defines a range of angles to be avoided. Note that also the range ±180 degrees is also avoided. The interval is defined in equatorial coordinates, from the celestial north to the +Y spacecraft axis (long axis of the bolometer), positive East of North, following the Position Angle convention. This effectively defines an avoidance angle for the satellite orientation, and hence it is a scheduling constraint.

Source Flux Estimates (optional):
An estimated source flux density (in mJy) may be entered for a band, in which case the expected S/N for that band will be reported back in the Time Estimation. The sensitivity results assume that a point source has zero background. If no value is given for a band, the corresponding S/N is not reported back.
Bright Source Setting (optional): this mode has to be selected if the expected flux of the source is above 200 Jy (see Section 4.1.2).

Time estimation and sensitivity

The SPIRE Point Source mode is optimised for observations of relatively bright isolated point sources. In this respect the accuracy of the measured flux is more relevant than the absolute sensitivity of the mode. The noise will be a function of three contributions. For a single ABBA repetition;

• The instrumental noise will be a constant value.

• There will be some underlying confusion noise which will vary from field to field.

• There will be a flux dependent uncertainty introduced by pointing jitter that will be some fraction of the total flux.

The current 1 σ instrumental noise uncertainties for a single ABBA repetition using the central co-aligned detector are tabulated in Table 3.2 and the HSpot screenshot is shown in Figure 3.12. The instrumental noise decreases as the reciprocal of the square root of the number of ABBA repetitions however note that the instrumental noise for a single repetition of this mode is expected to equal the extragalactic confusion noise, for sources fainter than 1 Jy.

Table 3.2: Point source mode sensitivities.

When to use this mode

The SPIRE Point Source mode is recommended for bright isolated sources in the range 0.2-4 Jy where the astrometry is accurately known and accurate flux measurement is required. For sources fainter than 200mJy (where the background produces a significant contribution) or at fluxes higher than ~ 4 Jy (where pointing jitter can introduce large errors) the Small Map mode is preferable.

For Point Source mode, the effective sky confusion level is increased due to chopping and nodding (by a factor of approximately 22% for the case of extragalactic confusion noise) and should be added in quadrature to the quoted instrumental noise levels. The result of the measurement is therefore affected by the specific characteristics of the sky background in the vicinity of the source and will depend on the chop/nod position angle in the event of an asymmetric background. Note that although it is possible to set a chop avoidance angle within HSpot this will constrain the possible dates for the observation

Figure 3.13: Example of possible chop area on a realistic background.

The example in Figure 3.13 shows a scan map observation of a ~ 220 mJy source. The circle drawn around the source corresponds to the chop and/or nod throw used in the Point Source mode. Moving around the circumference of the circle it is found the background can vary between ±30mJy depending on the chop/nod position angle used for the observation. Therefore, due to the problems of confusion noise, and the dependence of the result on the position angle of the observation, the point source AOT is not recommended for sources fainter than ~ 200 mJy, for which a small scan map will produce a better measurement including an accurate characterisation of the background.

For Point Source mode observations of bright sources (≥ 4 Jy) the uncertainties are dominated by pointing jitter and nod-position differences, resulting in a S/N of the order of 100 at most (the uncertainties in the data will also be limited by the accuracy of the flux calibration, which will be at least 5%). Users should be aware of these effects and take them into consideration.

3.3 SPIRE Spectrometer AOT

This observing mode is used to make spectroscopic observations with the SPIRE Fourier Transform Spectrometer (Section 2.3). The Spectrometer can be used to take spectra with different spectral resolutions:

• High resolution;

• Medium resolution;

• Low resolution;

• High and Low resolutions.

Spectra can be measured in a single pointing (using a set of detectors to sample the field of view of the instrument) or in larger maps which are made by moving the telescope in a raster. For either of these, it is possible to choose sparse, intermediate, or full Nyquist spatial sampling. In summary, to define an observation, one needs to select a spectral resolution (high, medium, low, high and low), an image sampling (sparse, intermediate, full) and a pointing mode (single or raster). These options are described in more detail in the next sections. For worked examples of how to combine these modes together to produce observations see Section 3.4.

The HSpot input parameters for all SPIRE Spectrometer observing modes are shown in Figure 3.14. In the following sections we describe each one of the options.

Figure 3.14: The HSpot initial screen for the SPIRE Spectrometer AOTs, point source mode (left) and raster (right)

3.3.1 Spectral Resolution

The Spectrometer Mirror Mechanism (SMEC) is scanned continuously at constant speed over different distances to give different spectral resolutions (see Section 2.3). For every repetition, two scans of the SMEC are done: one in the forward direction and one in the backward direction, making one scan pair, as shown in Figure 3.15. Two scan pairs are deemed essential for redundancy in the data. The desired integration time is set by increasing the number of scan pairs performed (corresponding to the number of repetitions entered in HSpot).

Figure 3.15: Diagram to show how the SMEC moves (in terms of optical path difference) during one repetition for High, Medium and Low spectral resolution. The low resolution SMEC scan range is always covered during High or Medium resolution observations.

Low Resolution:

Usage and Description: To make continuum measurements at the resolution of Δσ = 0.83 cm^-1 (λ∕Δλ = 48 at λ = 250μm, see Figure 4.3). The SMEC is scanned symmetrically about ZPD over a short distance. It takes 6.4 s to perform one scan in one direction at low resolution. This mode is intended to survey sources without spectral lines or very faint sources where only an SED is required.

Medium Resolution:

Usage and Description: The intermediate resolution of Δσ = 0.24 cm^-1 (λ∕Δλ = 160 at λ = 250μm, see Figure 4.3) will be more suited to broad features. Medium resolution scans are made by scanning the SMEC again symmetrically about ZPD, but over a larger distance than in the low resolution mode. It takes 24.4 s to perform one scan in one direction at medium resolution. This mode is intended for surveys where the user may require a significant amount of spatial coverage and also wishes to survey bright, isolated lines. For these cases the high resolution mode may take too much observing time. This mode may also be useful to characterise the SED with more data points than available with low spectral resolution.

High Resolution:

Usage and Description: The high resolution mode gives spectra at the highest resolution available with the SPIRE spectrometer, Δσ = 0.04 cm^-1 (1.2 GHz) which corresponds to λ∕Δλ = 1000 at λ = 250μm (see Figure 4.3). High resolution scans are made by scanning the SMEC to the maximum possible distance from ZPD. It takes 66.6 s to perform one scan in one direction at high resolution. This mode is best for discovery spectral surveys where the whole range from 194 to 671 μm can be surveyed for new lines. It is also useful for simultaneously observing sequences of spectral lines across the band (e.g. the CO rotational ladder). In this way, a relatively wide spectral range can be covered in a short amount of time compared to using HIFI (although with much lower spectral resolution than achieved by HIFI, see the HIFI Observers’ Manual).

The Instrumental Line Shape of the SPIRE spectrometer is a Sinc function (see Figure 4.2) and the FWHM of an unresolved spectral line will be 1.207 times the spectral resolution, i.e. 0.048 cm^-1 for a high resolution spectrum. The FWHM in km/s for the high and the medium resolution mode are shown in Figure 4.3.

Low resolution spectra are also extracted by the pipeline from high and medium resolution observations. Consequently, the equivalent low resolution continuum rms noise (for the number of scan repetitions chosen) can also be recovered from a high resolution observation – i.e. improving the sensitivity to the continuum.

For cases where the S/N ratio for this extracted low resolution spectrum is not sufficient for the scientific case, the following “High and Low” resolution mode is available:

High and Low Resolution:

Usage and Description: This mode allows to observe a high resolution spectrum as well as using additional integration time to increase the S/N of the low resolution continuum to a higher value than would be available from using a high resolution observation on its own. This mode saves overhead time over doing two separate observations.

The number of high resolution and low resolution scans can differ, and will depend on the required S/N for each resolution. If the number of repetitions for the high and low resolution parts are nH and nL respectively, then the achieved low resolution continuum sensitivity will correspond to nH+nL repetitions, because low resolution data can also be extracted from every high resolution scan.

It is up to the observer to decide if this mode, or a single high resolution observation is more suitable (in terms of sensitivities) for their scientific objectives. For examples of these considerations see Section 3.4.

3.3.2 Pointing Modes

A pointing mode and an image sampling are combined to produce the required sky coverage. Here the pointing modes are described.

Single Pointing Mode:

Usage and Description: This is used to take spectra of a region covered by the instrument field of view (2 arcmin diameter circle unvignetted). With one pointing of the telescope only the field of view of the arrays on the sky is observed.

Raster Pointing Mode:

Usage and Description: This is used to take spectra of a region larger than the field of view of the instrument (2 arcmin diameter circle unvignetted). The telescope is pointed to various positions making a hexagonally packed map (see example in Figure 3.16). At each position, spectra are taken at one or more BSM positions depending on the image sampling chosen (see Section 3.3.3). The HSpot input parameters are shown in Figure 3.14, right.

Details: The area to be covered determines the number of pointings in the map. The distances between individual pointings are 116 arcsec along the rows and 110 arcsec between the rows as shown in Figure 3.16. The number of pointings needed to cover the map is rounded up to ensure that the whole of the requested area is mapped. The area is by default centred on the target coordinates, however this can be modified by map centre offsets (given in array coordinates, see Photometer example of use of offsets Section 3.4).

Figure 3.16: Ratser map with the SPIRE FTS.

Note that for raster maps the target centre does not necessarily correspond to the centre of the detector array (see Figure 3.16). As the map is not circular and because the orientation of the array on the sky changes as Herschel moves in its orbit, the actual coverage of the map will rotate about the requested centre of the map (usually the target coordinates unless an offset is used) except for sources near the ecliptic (see the Herschel Observers’ Manual). To force the actual area to be observed to be fixed or to vary less, the Map Orientation settings of “Array with Sky Constraint” can be used to enter a pair of angles (which should be given in degrees East of North) to restrict the orientation of the rows of the map to be within the angles given.

Setting a Map Orientation constraint means that it will not be possible to perform the observation during certain time periods. Fewer days will be available to make that observation than the number of days that the target is visible (target visibility does not take into account the constraint as it is a constraint on the observation, not the target itself). In setting a constraint the observer will need to check that not all observing dates have been blocked and that it is still possible to schedule the observation. Note also that, as explained earlier, parts of the sky do not change their orientation with respect to the array and therefore it is not possible to set the orientation of the map in certain directions (the ecliptic) as the array is only orientated in one way on the sky. These constraints on when the observation can be performed make scheduling and the use of Herschel less efficient, hence the observer will be charged extra overheads to compensate.

Alternatively, raster observations can be split into several concatenated AORs to allow some tailoring of the coverage to match the source shape - see Section 3.4 for an example (but note that every concatenated AOR will be charged the 180 second slew tax).

User Input: The map parameters are similar to those for the Photometer Large Map. The Spectrometer parameters are listed in Section 3.3.4.

Figure 3.17: Spectrometer raster example to show spacing of the individual pointings for the long wavelength array (SLW, left) and the short wavelength array (SSW, right) for intermediate image sampling.

3.3.3 Image Sampling

The pointing and an image sampling mode are combined to produce the required sky coverage. Here the image sampling options are described and figures are given to show the sampling.

Note that the figures show only the unvignetted detectors. Detailed calibration for data from the non-central detectors will be more demanding than for the central detectors.

Figure 3.18: SPIRE Spectrometer spatial sampling: sparse (left), intermediate (centre) and full (right). The small green and magenta circles indicate the regions where spectra will be observed for different spatial samplings. The green circles show SSW and the magenta show SLW, the large red circle of 2 arcmin diameter is to guide the eye for the unvignetted field of view.

Sparse Image Sampling:

Usage and Description: In conjunction with a single pointing, to measure the spectrum of a point or compact source well centred on the central detectors of the Spectrometer. To provide sparse maps (either for a single pointing or a raster grid of pointings). The BSM is not moved during the observation, producing a single array footprint on the sky. The result is an observation of the selected source position plus a hexagonal-pattern sparse map of the surrounding region with beam centre spacing of (32.5, 50.5) arcsec in the (SSW, SLW) bands as shown in Figure 3.18. For a point source this requires accurate pointing and reliable knowledge of the source position to be sure to have the source well centred in the (central) detector beam.

Intermediate Image Sampling:

Usage and Description: This is to produce imaging spectroscopy with intermediate spatial sampling (1 beam spacing). This gives intermediate spatial sampling without taking as long as a fully Nyquist sampled map. This is achieved by moving the BSM in a 4-point low frequency jiggle, giving a beam spacing of (16.3, 25.3) arcsec in the final map as shown in Figure 3.18 and Figure 3.19. The input number of repetitions is performed at each of the 4 positions to produce the spectra. The coverage maps for the SSW and SLW in this mode are shown in Figure 3.20, left column.

Full Image Sampling:

Usage and Description: This allows fully Nyquist sampled imaging spectroscopy of a region of the sky or an extended source. This is achieved by moving the BSM in a 16-point jiggle to provide complete Nyquist sampling (1/2 beam spacing) of the required area. The beam spacing in the final map is (8.1, 12.7) arcsec as shown in Figure 3.18 and in Figure 3.19. The input number of repetitions is performed at each one of the 16 positions to produce the spectra. The coverage maps for the SSW and SLW in this mode are shown in Figure 3.20, right column.

Figure 3.19: The FTS mapping with intermediate image sampling for SSW and SLW (4-point jiggle, top) and full sampling (16 point jiggle, bottom). The red circle shows the 2’ unvignetted field of view of the FTS.

3.3.4 User input parameters for all Spectrometer AOTs.

The user inputs shown in Figure 3.14 are given below:

Pointing Mode:
Single Pointing or Raster selection. See Section 3.3.2 for details. Note that if Raster is selected then size of the map (Length and Height) must be given.

Image Sampling:
Sparse, Intermediate or Full. See Section 3.3.3 for details.

Spectral Resolution:
High, Medium, Low or High and Low. See Section 3.3.1 for details.

Repetition factor:
The number of spectral scan pairs to be made at each position. Note that if High and Low resolution is selected you can independently control the number of pairs for each resolution.

Length:
In arcmin. The length of the raster map along the rows.

Height:
In arcmin. The height of the raster map.

Map centre offset Y, Z:
In arcmin. The offset of the raster map centre from the input target coordinates along the Y or Z axes of the arrays. Minimum is ±0.1 arcmin, maximum ±300 arcmin.

Map Orientation:
Either Array or Array with Sky Constraint. If Array with Sky Constraint is selected then range of the map orientation is constrained. This is a scheduling constraint and should therefore only be used if necessary.

Angle from/to:
In degrees East of North. In the case that Array with Sky Constraint is selected, the angles between which the raster rows can be constrained to are entered here.

Source Flux Estimates:
Optional: if the estimated line flux in 10^-17 W/m², and/or the estimated continuum (selectable units either Jy or 10^-17 W/m²/μm) is entered along with a wavelength then the expected S/N for that wavelength will be reported back in the Time Estimation as well as the original values entered. The time estimator always returns 1-σ flux sensitivity, 1-σ continuum sensitivity and unapodised resolving power for 8 standard wavelengths. Note, when Low resolution is selected only continuum information can be entered and returned (plus the unapodised resolving power). When High and Low resolution is selected data are returned for the two different resolutions.

Figure 3.20: Intermediate (top) and Full (bottom) spatial sampling coverage maps for SLW (left) and SSW (right) from a real SPIRE FTS mapping observation. The sky spectral pixel (spaxel) sizes are 35 arcsec (top left), 17.5 arcsec (bottom left), 19 arcsec (top right), 9.5 arcsec (bottom right). The number of bolometer hits in each sky pixel are encoded with colour. The holes in the maps, due to dead bolometers, depend on the spacecraft attitude (the focal plane position angle), the grid centre, the pixel scale.

Bright source mode:
Optional: when the source is expected to be very bright (see Section 5.3.4 for more details) then this option provides a way to switch the detectors to bright mode settings, thus avoiding signal clipping. Using this mode leads to 25 s increase in the overhead time, because the detector A/C offsets are set at the start of the observation at each jiggle position.

3.4 Using HSpot to prepare AOR

This section lists screencast tutorials available as an on-line material from the HSC web pages. Note that the video tutorials are without an audio recording.

• Photometer observations

  • Small Map AOR:
    In this tutorial: how to fill in a target, change AOR label, check visibility, check the time estimation and achieved sensitivity, input estimated flux for the source to get the S/N, overlay the AOR on an image.
    http://herschel.esac.esa.int/Docs/SPIRE/Videos/small-map-video.mov

  • Large Map AOR:
    In this tutorial: how to fill in a target, change AOR label, check visibility, check the time estimation and achieved sensitivity, overlay the AOR on an image, set map orientation constraints.
    http://herschel.esac.esa.int/Docs/SPIRE/Videos/large-map-video.mov

  • Point Source AOR:
    In this tutorial: how to fill in a target, change AOR label, check visibility, check the time estimation and achieved sensitivity, input estimated flux for the source to get the S/N, overlay the AOR on an image, set up chop avoidance angles.
    http://herschel.esac.esa.int/Docs/SPIRE/Videos/point-source-video.mov

• Spectrometer observations

  • Point source, sparse map AOR:
    In this tutorial: how to fill in a target, change AOR label, check visibility and background, check the time estimation and achieved sensitivity, input estimated flux for the source to get the S/N, overlay the AOR on an image.
    http://herschel.esac.esa.int/Docs/SPIRE/Videos/fts-sparse-video.mov

Chapter 4
SPIRE in-flight performance

The performance of SPIRE was estimated prior to launch using a detailed model of the instrument and the telescope and the results of instrument-level and Herschel system-level tests. Some details of the model assumptions and adopted parameters are given in e.g., Griffin (2008). Based on the optimisation and evaluation of the instrument performance during Commissioning and Performance Verification phases, and further checks using Science Demonstration phase observations, the in-flight performance of the photometer and FTS have now been assessed, and HSpot has been updated accordingly. In this section we summarise the achieved in-flight performance.

4.1 Photometer performance

4.1.1 Beam profiles

The photometer beam profiles have been measured using scan maps of Neptune, which provides high S/N and appears point-like in all bands. The beams are well described by 2-D Gaussians down to ~ 15 dB, with FWHM values and detailed side-lobe structure in good agreement with the pre-launch optical model of the instrument and telescope system. The basic beam parameters vary as a function of the pixel scale used in the beam map, with the FWHM values and beam areas increasing with pixel size as the fidelity of the surface brightness reconstruction becomes less reliable at low resolution, particularly with respect to the Airy ring pattern at higher radii from the source peak. The basic beam parameters, determined by fitting a 2-D asymmetric Gaussian to the data binned into pixels of 1 arcsec side and pixels of the standard sizes used for SPIRE Level-2 maps (6, 10, 14) arcsec per pixel at (250, 350, 500) μm are given in Table 4.1. These figures represent an average over each array; there are small systematic variations at the level of ~  5% across the arrays.

The beam maps and parameters, and their use in calibration of extended emission in SPIRE maps, are described in more detail in Chapter 5.

Table 4.1: Basic Gaussian parameters for measured beams with a 1 arcsec pixel size and for the nominal SPIRE Level-2 map pixel sizes (6, 10, 14)”. Uncertainties in the beam FWHM values and areas are estimated at < 1%. See Section 5.2.7 for more details.

4.1.2 Sensitivity

The photometer sensitivity in scan map mode has been estimated from repeated scan maps of dark regions of extragalactic sky. A single map repeat is constituted by two orthogonal scans as implemented in the SPIRE-only scan-map AOT. Multiple repeats produce a map dominated by the fixed-pattern sky confusion noise, with the instrument noise having integrated down to a negligible value. This sky map can then be subtracted from individual repeats to estimate the instrument noise. The extragalactic confusion noise levels for SPIRE are assessed in detail by Nguyen et al. (2010), who define confusion noise as the standard deviation of the flux density in the map in the limit of zero instrument noise. The measured extragalactic confusion and instrument noise levels are given in Table 4.2 for the nominal scan speed (30′′/s). Instrument noise integrates down in proportion to the square root of the number of repetitions, and for the fast scan speed (60′′/s) the instrument noise is higher as expected from the factor of 2 reduction in integration time per repeat. The achieved instrument noise levels are comparable to the pre-launch estimates which were (9.6, 13.2, 11.2) mJy in beam at (250, 350, and 500) μm – very similar for the 250 and 500 μm bands and somewhat better for the 350 μm band. In SPIRE-PACS Parallel mode, the achieved SPIRE instrument noise level per repeat is different to that for a single repeat in SPIRE-only mode due to the different effective integration time per beam (see the SPIRE-PACS Parallel Mode Observers’ Manual).

Figure 4.1: Pixel noise vs. integration time for all pixels in deep SPIRE photometer fields. The derived instrument noise is shown in red, the confusion floor is show in blue and the total noise is in green. Taken from Nguyen et al. (2010).

Figure 4.1 shows the manner in which the overall noise integrates down as a function of repeats for cross-linked maps with the nominal 30′′/s scan rate. The overall noise is within a factor of of the (250, 350, 500) μm confusion levels for (3, 2, 2) repeats.

Table 4.2: Estimated SPIRE Photometer sensitivities. For the Parallel mode sensitivities please consult the The SPIRE-PACS Parallel Mode Observers’ Manual.

Notes:

1. All sensitivity values correspond to nominal source strength settings. For bright source settings, recommended for sources brighter than 200 Jy in any band, the achieved sensitivities are degraded (with respect to nominal setting) by factors of (3.8, 3.2, 2.6) for (250, 350, 500) μm. It should be noted however, that in practice S/N values > 200 should not be regarded as reliable in any case.

2. All scan map sensitivity values are for nominal scan speed of 30”/s. Figures for 60”/s scale as .

3. For Point Source mode (7-point jiggle) observations, the effective sky confusion level is increased due to chopping and nodding. The result of the measurement is therefore affected by the detailed characteristics of the sky background in the vicinity of the source and will depend on the chop/nod position angle in the event of an asymmetric background. In the absence of a source, the flux density returned by the pipeline for the measurement corresponds to the difference between the background at the source position and the average flux density of the nearby positions sampled in the measurement. For example, for observations of a source against a background of extragalactic sky, the uncertainty due to confusion is on the order of times the 1-σ confusion noise levels noted above, corresponding to 8-10 mJy. This should be added in quadrature to the instrument noise levels quoted for the point source observation. Users should be aware of this effect and take this into account. Because of the problem of confusion noise, and the dependence of the result on the position angle of the observation, the Point Source (7-point jiggle) AOT is not recommended for sources fainter than ~ 200 mJy, for which a small scan map will produce a better measurement including an accurate characterisation of the background. For observations of bright sources (> a few Jy) the uncertainties are dominated by pointing jitter and nod-position differences, resulting in a S/N on the order of 100 at most.

An important aspect of the photometer noise performance is the knee frequency that characterises the 1∕f noise of the detector channels. Pre-launch, a requirement of 100 mHz with a goal of 30 mHz had been specified. In flight, the major contributor to low frequency noise is temperature drift of the ³He cooler. Active control of this temperature, available via a heater-thermometer PID control system, has not been implemented in standard AOT operation as trials have shown that a better solution, in terms of overall noise performance, is to apply a temperature drift correction in the data processing. The scan-map pipeline includes a temperature drift correction using thermometers, located on each of the arrays, which are not sensitive to the sky signal but track the thermal drifts. This correction works well and has been further improved with the recent update of the flux calibration parameters. Detector timelines to de-correlate thermal drifts over a complete observation can produce a 1∕f knee of as low as a 1-3 mHz. This corresponds to a spatial scale of several degrees at the nominal scan speed.

As with most observing systems, high S/N predictions should not be taken as quantitatively correct. This is because small errors such as pointing jitter, other minor fluctuations in the system, or relative calibration errors, will then become significant. That is why a signal-to-noise of 200 is taken as the maximum achievable for any observation, and HSpot will never return a value of S/N greater than 200.

4.1.3 Observing overheads

Scan-map mode is very efficient for large area observations, but somewhat less so for smaller fields due to the time needed to turn the telescope around at the end of each scan leg. HSpot provides a summary of the on-source integration time and the various overheads for any particular observation. For example, a 2deg ×2deg scan map with the nominal speed and two repeats takes a total of 7.4 hrs (including all instrument and telescope overheads) with an overall efficiency of 86%. For a 20 × 20 arcmin map with two repeats, the duration is 31 min. with an overall efficiency of 51% due to the larger fraction of time spent in turning around the telescope. For the Small Map AOT (approx. 5 × 5 arcmin map area), with two repeats, the duration is ~ 8 min. with an efficiency of 15% (but the total observing time still has a large relative contribution from the 3 min. telescope slewing overhead).

4.1.4 Some HSpot examples

A full description of HSpot and its use is given in The HSpot Users’ Guide and a number of examples for preparing observation requests are given in Section 3.4. Here we provide a few examples to indicate some kinds of observations that may become standard for many purposes.

Point source photometry

For many point source observations, the following standard parameters are adopted:

Note that this produces rms instrument noise levels that are already lower than the extragalactic confusion limits.

Small scan map

Small scan map observations cover an approximately 5 arcmin diameter circular area. The following are typical examples:

With two repeats, the rms flux density limits due to instrument noise are already getting close to the confusion limits. So one or two repeats should be adequate for most Small Map observations.

Large scan map

Maps larger than 5 arcmin in diameter are executed in Large Map mode. The default large map mode is to perform cross-linked scans in two orthogonal scan directions. Some examples are given below for the two different scan speeds: nominal (30′′/s) and fast (60′′/s). The repetition factor refers to the number of A+B pairs.

From these examples one can see that:

• the sensitivity for one map repeat does not depend on the map size so it is necessary to increase the repetition factor in order to achieve better resolution.

• fast scanning mode makes sense only for large maps (several square degrees) because for small areas the overheads are too large making the observation too inefficient.

4.2 Spectrometer

4.2.1 Spectral range, line shape and spectral resolution

Table 4.3 summarises the spectral range, and spectral resolution characteristics of the FTS.

Table 4.3: Spectral range over which FTS data can currently be calibrated.

The FTS spectral range given in Table 4.3 represents the region over which the FTS sensitivity estimates and calibration can be considered reliable at this time. Data will be provided extending beyond the longer-wavelength end of the range, out to 685 μm. Users should be cautious in the interpretation of any such data.

The resolving power σ∕Δσ = λ∕Δλ is shown in Figure 4.3 for the three standard spectral resolutions shown in Table 4.4.

Table 4.4: Spectral resolution and line FWHM for high and low resolution modes.

The instrumental line shape of all FTS instruments is a Sinc function due to the truncation of the interferogram by the limited travel of the moving mirror (the SMEC). For the Sinc function, shown in Figure 4.2, the spectral resolution is defined to be the distance from the peak to the first zero crossing, i.e. Δσ = 1∕(2L), where L is the maximum optical path difference created by the scan mirror travel. The line FWHM is given by 1.20671 × Δσ. The corresponding FWHM in km s-1 is

Figure 4.3 shows the corresponding FWHM for high and medium spectral resolution. For example, for high spectral resolution, the line FWHM in km s-1 for the SSW and SLW is between 280-450 km s-1 and 440-970 km s-1 respectively.

Figure 4.2: The FTS instrumental line shape, the sinc function.

The spectral range and spectral resolution for the central detectors (SSWD4 and SLWC3, see Figure 2.7) also applies to the other detectors across the spectrometer arrays used for spectral mapping.

Figure 4.3: The unapodised resolving power of the FTS for three standard spectrometer resolutions (see Section 3.3). The SSW is in blue, while the SLW is in red (left). The corresponding line FWHM in km s-1 for the high (HR) and medium (MR) resolution modes (right).

4.2.2 Wavelength scale accuracy

The FTS wavelength scale accuracy has been verified using line fits to the ¹²CO lines in five Galactic sources with the theoretical instrumental line shape (Sinc profile). The line centroid can be determined to within a small fraction (~ 1∕20^th) of the spectral resolution element if the signal-to-noise is high. There is a very good agreement between the different sources and across both FTS bands.

4.2.3 Beam profiles

The FTS beam size and shape varies as a function of frequency across the bands, and cannot be characterised by a simple Gaussian response. This is as expected from the multi-moded feedhorns used for the spectrometer arrays, as different detector feedhorn/waveguide modes become important at certain frequencies in the band (the number of propagated modes increases with frequency). The effect is most prominent for the SLW band which covers a rather broad spectral range and is single-moded at its long-wavelength end but multi-moded at its short-wavelength end.

The beam properties as a function of wavelength have been characterised by taking medium resolution spectra on a point source (Neptune) placed at different locations within the beam by stepping the satellite position. A detailed summary of the results is given, and the implications for FTS flux calibration are discussed in Section 5.3.1.

4.2.4 Sensitivity

The FTS sensitivity achieved to date for a point source observation is summarised in Table 4.5, which assumes unapodised spectra. The integrated line flux sensitivity is plotted vs. wavelength in Figure 4.4 for unapodised spectra. For the standard recommended apodization (the extended Norton-Beer function 1.5; Naylor & Tahic 2007), the sensitivity is improved by a factor of ~ 1.5 at the expense of a broadening of the spectral resolution element by a similar factor. Whilst this is not advisable for crowded spectra, it may provide better results for weak isolated lines.

In principle, the integrated line flux sensitivity is independent of the spectral resolution. In practice, only high resolution mode should be adopted for line observations. For an FTS, the limiting sensitivity for the continuum scales as the reciprocal of the spectral resolution, and the medium and low-resolution sensitivities in Table 4.5 are thus scaled by factors of 6 (= 0.24/0.04) and 21 (= 0.83/0.04), respectively.

The (5-σ; 1 hr) limiting integrated line flux is typically 1.5 × 10^-17 W m^-2 for both SSW and SLW bands. With currently available data processing, the noise level continues to integrate down as expected for at least 100 repeats (i.e., 100 forward and 100 reverse scans; total on-source integration time ~ 4 hours). Note that this is a considerable improvement with respect to the quoted performance in v2.1 of this document and in Griffin et al. (2010). The achieved FTS sensitivity is better than pre-launch predictions by a factor of 1.5-2. This is attributable to the low telescope background, the fact that the SCAL source is not used, and to a conservatism factor that was applied to the modelled sensitivities to account for various uncertainties in the sensitivity model.

It should be noted, however, that achieving the nominal continuum sensitivity level for low-resolution observations of faint sources (less than ~ 1 Jy) cannot be relied upon as yet due to the difficulty in achieving correct subtraction of the thermal emission from the telescope and from the ~ 5 K instrument enclosure.

Table 4.5: FTS point source sensitivity (unapodized) for high resolution (HR, Δσ = 0.04 cm^-1), medium resolution (MR, Δσ = 0.24 cm^-1) and low resolution (LR, Δσ = 0.83 cm^-1).

Figure 4.4: FTS point source line flux sensitivity (unapodized) vs. wavenumber across the FTS bands.

A number of important points concerning the FTS sensitivity should be noted.

1. The integrated line flux sensitivity for an unresolved line is in principle independent of the resolution for an FTS, so the high-resolution sensitivities also apply to medium resolution mode. In practice the performance is better for high resolution mode, and this is strongly recommended for sensitive line spectroscopy.

2. For point source observations, a sparse map covering the full FTS field of view is also generated. The full field of view is 2.6 arcmin diameter, but the outer ring of detectors is partially vignetted. The unvignetted field of view is specified as 2 arcmin. Data from the full field of view are available, but the accurate calibration of the outer parts cannot be guaranteed at this time.

3. For very strong sources, a bright-source mode is available, for which the sensitivity is reduced compared to nominal mode by a factors of approximately 2 for the SLW array and 4 for the SSW array. Guidance on use of the bright source mode is provided in Section 5.3.4.

4. As for the photometer, the maximum achievable S/N should be taken as 200.

5. For spectral mapping:

   1. Integrated line flux sensitivity is essentially the same as for point source for a given map point (in terms of W m^-2 in beam).

   2. For a fully sampled map, spatial pixels in the spectral cube can be co-added/resized to enhance sensitivity (as in the photometer), but it is best to assume no enhancement in sensitivity as calibration errors or other imperfections may counteract the gain available in principle.

Continuum calibration should be cross-checked by including a map with the photometer in the programme (this will generally occupy only a small fraction of the time for the FTS observations).

4.2.5 Some HSpot Examples

Note that the observing overheads are much smaller than for any of the photometer modes as the telescope is not moved in the course of the observation.

Chapter 5
Flux Density Calibration

5.1 Calibration sources and models

SPIRE flux calibration is based on Neptune for the photometer and primarily on Uranus for the spectrometer. The SPIRE calibration programme also includes observations of Mars, asteroids, and stars to enable a consistent and reliable flux calibration to be developed over the course of the mission, and to ensure that cross calibration with PACS and HIFI, and with other facilities, is well established. The currently assumed asteroid and stellar models are briefly described below for information.

5.1.1 Neptune and Uranus angular sizes and solid angles

The adopted equatorial radii (1-bar level) and eccentricities for Uranus and Neptune are summarised in Table 5.1 and are based on the analysis of Voyager data by Lindal et al. (1987) and Lindal (1992). These are similar to the values used in the ground-based observations by Griffin & Orton (1993), Hildebrand et al. (1985) and Orton et al. (1986).

Table 5.1: Adopted planetary radii and eccentricity values.

In calculating the planetary angular sizes and solid angles, a correction is applied for the inclination of the planet’s axis at the time of observation, and the apparent polar radius is given by (Marth, 1897):

where ϕ is the latitude of the sub-Earth point, and e is the planet’s eccentricity:

The observed planetary disc is taken to have a geometric mean radius, r_gm, given by

For a Herschel-planet distance of D_H, the observed angular radius, θ_p, and solid angle, Ω, are thus

Typical angular radii for Uranus and Neptune are 1.7 arcsec and 1.1 arcsec respectively.

5.1.2 Neptune and Uranus models

Models of Uranus and Neptune by Moreno (1998, 2010) have been agreed by the Herschel Calibration Steering Group (HCalSG) as the current standards for Herschel, and are available on the HCS calibration ftp site1 . The Uranus and Neptune disk-averaged brightness temperature spectra are plotted in Figure 5.1. In the Herschel range, the disk averaged brightness temperatures increase with wavelength as deeper layers in the atmosphere are probed. The planets have similar temperatures, despite Neptune’s greater distance from the Sun, because Neptune has an internal heat source. This also leads to a more dynamic neptunian atmosphere resulting in some prominent spectral features whereas the Uranian spectrum is largely featureless.

Typical photometer (250, 350, 500) μm calibration flux densities (see Section 5.2 for precise definition) are (160, 100, 60) Jy for Neptune and (370, 250, 150) Jy for Uranus.

The Uranus and Neptune models are currently quoted as accurate to ±5%. Note that the models currently used for SPIRE are the “esa-2” tabulations. These may be subject to change as knowledge of the atmospheric properties becomes more refined, based on Herschel and other observations. Any such changes will be assessed and authorised by the HCalSG, and corresponding updates to the SPIRE and PACS flux calibration will be released accordingly .

Figure 5.1: Currently adopted models (Moreno, 2010) of the brightness temperature spectra of Uranus and Neptune.

5.1.3 Mars models

Web-based models of the martian continuum by Emmanuel Lellouch and Bryan Butler are available at http://www.lesia.obspm.fr/perso/emmanuel-lellouch/mars/ and http://www.aoc.nrao.edu/~bbutler/work/mars/model/.

Mars is a very bright source for SPIRE. For example, at the time of its observation by SPIRE on OD 168 (29 Oct. 2009) it had flux densities of (9300, 5000, 2500) Jy at (250, 350, 500) μm. The nominal Herschel telescope background is equivalent to approximately (230, 250, 270) Jy, so that Mars is equivalent to (40, 20, 10) time the nominal telescope brightness.

5.1.4 Asteroid models

The larger asteroids can also be used as FIR/submillimetre calibration sources, and were particularly important in the early part of the mission when Uranus and Neptune were not visible. The most accurate asteroid models are the thermophysical models of Müller & Lagerros (2002), which have been tabulated by Müller (2009) and must be computed in detail for a given observation date and time (there can be significant variations in brightness associated with the asteroid rotation period). For planning and estimation purposes, the asteroid Standard Thermal Model (STM) (Lebofsky et al., 1986) can be used to estimate the expected flux densities.

As an illustration, STM spectra for Dec. 9 2009 are shown in Figure 5.2 for the four largest asteroids, 1-Ceres, 2-Pallas, 3-Juno, and 4-Vesta. Note that STM asteroid spectra are all of approximately the same shape, close to that of a Rayleigh-Jeans black body: the monochromatic flux density ratios are typically 1.98 for S₃₅₀∕S₅₀₀ and 3.7–3.8 for S₂₅₀∕S₅₀₀.

The initial SPIRE photometer flux calibration was based on observations of 1-Ceres on OD50 (02 July 2009), for which the Ceres thermal spectrum was derived using the STM. This initial calibration has now been superseded by the Neptune-based calibration. The changes to the flux calibration scale are quite small, but the uncertainties are now much improved2 .

Figure 5.2: Standard Thermal Model spectra of 1-Ceres, 2-Pallas, 3-Juno, and 4-Vesta for Dec. 9 2009.

5.1.5 Stellar calibrators

At present, the PACS photometer calibration is based on a set of standard stars identified by the HCalSG. These stars are also being observed by SPIRE as part of the SPIRE-PACS cross calibration programme, which will include detailed comparison of the stellar-based and Neptune-based calibrations. The eight stars are: α Boo, α Tau, γ And, β Peg, γ Dra, Sirius, and α Cet.

Model spectra for these stars have been generated by Leen Decin based on the MARCS stellar atmosphere code of Decin & Eriksson (2007), covering 2-200 μm, and the data are available from within the Herschel Interactive Processing Environment3 . The quoted estimated uncertainty is 1% for that wavelength range. Figure 5.3 shows the model FIR SEDs for the eight stellar calibrators with extrapolations to the SPIRE photometer bands based on the spectral index in the 150-200 μm range. The latter is fairly uniform, varying between -1.99 and -2.034 for the eight sources. Computations covering wavelengths up to 700 μm are awaited. In the meantime, the available SEDs can be extrapolated with reasonable accuracy to SPIRE wavelengths, assuming no excess emission due to a chromospheric component or to a cold dust component around the star. The presence of any such excess would lead to a higher flux density, so the extrapolated figures can be taken as lower limits.

Figure 5.3: Decin & Eriksson (2007) FIR SEDs model for the eight stellar calibrators with extrapolations to the SPIRE photometer bands.

5.2 Photometer flux calibration scheme

The photometer pipeline produces monochromatic in-beam flux densities (Jy/beam) at standard frequencies corresponding to 250, 350 and 500 μm, and calculated under the assumptions of (i) a point source observation and (ii) a flat νS_ν spectrum. The calibration is carried out at the level of the detector timelines (Level-1 data products). The SPIRE Level-2 photometer products (maps) are also calibrated in terms of in-beam flux density (Jy/beam) rather than surface brightness (Jy/pixel or /sr).

The primary calibration standard is Neptune (Moreno 2010 model) which has an estimated absolute uncertainty of 5%. The detailed computations, and the appropriate corrections for an extended source or to convert to a different assumed source spectrum, are described in this section.

5.2.1 Photometer Relative Spectral Response Function

In a SPIRE photometer observation, the property of the source that is directly proportional to source power absorbed by the bolometer is the integral over the passband of the flux density weighted by the instrument Relative Spectral Response Function (RSRF), as indicated in Figure 5.4:

where S_S(ν) represents the in-beam source flux density at the telescope aperture and R(ν) is the RSRF.

Figure 5.4: RSRF-weighted flux density defined as the integral of the source spectrum weighted by the instrument RSRF

The three photometer RSRFs are shown in Figure 5.5. The thick lines correspond to the overall filter transmission functions, and give the RSRFs, R_P (ν), for the case of a point source. The thin lines are the RSRFs for an extended source, R_E(ν). An extended source is defined here as a source that fills the entire beam solid angle with a uniform surface brightness4 . The extended source profiles are derived by weighting the point source RSRFs by λ² to take into account the single-mode coupling via the feedhorns. This λ² weighting effectively takes into account the fact that the beam width varies across the band in proportion to λ, leading to a larger beam area at longer wavelengths and so additional power coupled from extended emission. Note that the absolute vertical scale in Figure 5.5 is irrelevant to the computations in this note as all relevant parameters involve ratios of RSRF integrals. The RSRF curves can be accessed from the SPIRE Calibration Tree in the Herschel Interactive Processing Environment (HIPE) and also from the HSC ftp.5

Figure 5.5: Photometer RSRFs: R_P (ν) (thick lines; point source; no weighting of filter transmission profiles) R_E(ν) (thin lines; extended source; λ² weighting). The wavelength scale on the top is given for reference.

5.2.2 Calibration flux densities

Let the RSRF for a point source observation be R_P (ν) and that for an extended source be R_E(ν) (as shown in Figure 5.5, right). The standard calibration source, Neptune, is small (diameter < 2.5 arcsec) compared to the SPIRE beam widths, so R_P (ν) is the appropriate RSRF.

When observing a calibration source, the property that is directly proportional to absorbed detector power is

where S_C is the calibrator flux density at the telescope aperture and K_Beam is a correction factor for partial resolution of the calibrator by the telescope beam. For a Gaussian beam profile coupling to a uniformly bright disk (planet or asteroid), the beam correction factor is given by (Ulich & Haas, 1976):

where θ_p is the angular radius of the disk, and θ_Beam is the beam FWHM. The corresponding (250, 350, 500) μm beam correction factors are small: (0.988, 0.994, 0.997) for Uranus and (0.995, 0.997, 0.999) for Neptune.

S_Calib for Neptune has been used in the derivation of the flux density conversion module parameters that are applied in the pipeline, and which are in turn used to derive the RSRF-weighted source flux density S_S.

5.2.3 Response of a SPIRE bolometer to incident power

The output signal voltage of a SPIRE bolometer depends on the absorbed signal power, which is in turn a function of the source power collected by the telescope. For NTD bolometers with a given applied bias voltage, the small-signal responsivity varies with the voltage across the bolometer with an approximately linear relationship over a wide range of background loading and bath temperature conditions. This translates to a corresponding relationship for the differential sensitivity of the system to the RSRF-weighted flux density, S:

To allow for the fact that the responsivity-operating point voltage relationship will not be exactly linear, we let

Note that:

1. f(V ) is specific to a particular bolometer and bias setting;

2. f(V ) is negative (since absorbed power causes a decrease in bolometer voltage); however, in the rest of this document we take it to be positive for convenience, assuming that a correction factor of -1 is applied.

In order to perform conveniently the integration of f(V ), an appropriate function can be fitted to it. Various fitting functions have been investigated and it is found that the most suitable function is of the form:

where K₁, K₂ and K₃ are constants. K₁ has units of Jy V^-1, K₂ has units of Jy, and K₃ has units of V.

An example plot of f(V ) vs. V is shown Figure 5.6, and corresponds to a typical SPIRE 350 μm bolometer. The nominal operating point (blank sky) in this case would be close to 3 mV, and the range covered by the plot covers a sky brightness range up to more than 10 times the telescope brightness. The blue points are derived from a bolometer model, and the red line corresponds to the best fit K-parameters using equation 5.10.

Figure 5.6: Typical plot of f(V ) vs. V (for a nominal 350 μm bolometer). The blue points correspond to the bolometer model and the red line is the fitted function using equation 5.10.

A flux density corresponding to a measured RMS bolometer voltage, V _m, can be derived by integrating the above expression between some fixed bolometer voltage, V ₀, and V _m:

so

Ideally, V ₀ would be the bolometer voltage in the absence of any astronomical signal (i.e., what would be measured when observing blank sky in otherwise identical conditions). The resulting flux density would correspond to that from the sky calibrated with respect to the blank sky level. V ₀ is therefore derived from standard calibration observations of a “dark” area of sky in scan-map mode under the nominal conditions: bias voltage and frequency, bolometer and instrument FPU (Level-1) temperature, and telescope temperature. Ideally the conditions would be the same for the calibration and science observations but small differences are inevitable in practice. V ₀ thus differs from the ideal value (by an amount much larger than most astronomical signals). This means that the raw flux density values produced by the pipeline have additive offsets (different for each bolometer) that must be removed before map-making to derive the flux density from the sky.

Values of K₁, K₂ and K₃ have been derived from calibration observations, and are used in the pipeline flux conversion module together with the K_4P parameter (see the next subsection) to produce the SPIRE flux density timelines.

5.2.4 Conversion of RSRF-weighted flux density to monochromatic flux density

Definition of a monochromatic flux density requires the adoption of a standard frequency for the band and some assumption about the shape of the source spectrum. The approach adopted for SPIRE and PACS is to assume that the spectrum is a power law across the band defined by the flux density at a standard frequency ν₀ , and a spectral index α_S:

The convention adopted for Herschel is to adopt α_S = α_S0 = -1 (corresponding to νS_ν flat across the band). For SPIRE, we choose values of ν₀ to correspond to wavelengths of 250, 350 and 500 μm for the three bands, and monochromatic flux densities at those frequencies are generated by the pipeline.

Under this assumption, the measured RSRF-weighted flux density (to which the bolometer output voltage due to the source is proportional in the linear regime) is thus

where R(ν) = R_P (ν) for a point source or R_E(ν) for an extended source.

The source flux density at frequency ν₀, which is produced by the pipeline, is therefore given by:

The measured RSRF-weighted flux density is thus multiplied by K₄ to derive the monochromatic flux density at the standard wavelength to be quoted to the user.

Putting α_S = -1 gives

Note that the values of K₄ are different for point and extended sources:

and

The SPIRE photometer pipeline is based on the point source case and so uses K_4P in the voltage-to-flux density conversion. To derive the flux density for an extended source, the pipeline output must be multiplied by K_4E∕K_4P . In addition, a colour correction is usually required, the procedure for which is given in Sections 5.2.5 and 5.2.9.

5.2.5 Colour correction

The assumption that the source has a spectrum with νS_ν flat across the band (α_S0 = -1) will not be the case for most observations. For instance, at SPIRE wavelengths, planets and other solar system objects will typically have a spectral index of 2 (corresponding to black body emission in the Rayleigh-Jeans region). Dust sources will typically have a steeper spectrum, with α_S0 = 3 - 4. For the highest calibration accuracy a colour correction can be applied by the astronomer based on other information (for instance, measurements in other SPIRE or PACS bands and/or data from other telescopes). Depending on the nature and temperature of the source, the true spectral index could be different for the three SPIRE bands, as illustrated in Figure 5.7, which could apply in the case of a cold dust source.

Figure 5.7: Illustration of the possibility of different source spectral indices for the three SPIRE bands.

Given the width of the SPIRE bands and the nature of the observed source SEDs, in most cases it will be appropriate to assume that the source spectrum follows a power law across the band, but with a different spectral index, α_Snew. Let S′_S(ν₀) be the source flux density at ν₀ for that spectral shape. We then have from equation 5.15

Putting α_S0 = -1 gives

Once again, K_C is different for point and extended sources due to the different RSRFs. The colour correction factors for SPIRE are given in Section 5.2.8, and an example of how to apply the colour correction is given in Section 5.2.9.

5.2.6 Conversion of in-beam flux density to surface brightness

The in-beam astronomical flux density at a given frequency, ν, is defined as:

where θ ∈ [0,π] is a radial angular offset from the beam centre, ϕ ∈ [0,2π] is an azimuthal angular offset, B(θ,ϕ) is the normalised beam profile, I_ν(θ,ϕ) is the sky intensity (surface brightness) profile, and dΩ is a solid angle element in the direction defined by (θ,ϕ). Note that we assume here that the beam profile can be regarded as uniform across the spectral passband (the effect of beam profile variation across the band is taken into account by the extended source RSRF, as described in Section 5.2.1).

The pipeline produced flux densities in terms of Jy in-beam. For an extended sources which is uniformly bright over the beam area (solid angle), the surface brightness (Jy arcsec^-2 or Jy sr^-1) can be obtained from the flux density by dividing it by the beam area.

The beam area is

For a Gaussian beam profile with FWHM θ_Beam, the beam area is given by

However, the SPIRE beams exhibit departures from Gaussianity at low levels due to the diffraction effects of the central obscuration and the secondary supports, and it is important to use the full beam area in the conversion, as explained in Section 5.2.7

5.2.7 Photometer beam maps and areas

Updated SPIRE photometer beam data and accompanying detailed information are available at the HSC calibration ftp site6 and comprise the following:

• new empirical beam maps based on fine-scan-map measurements of Neptune;

• the raw data used for the above;

• a theoretical model including coverage of the sidelobes and low-level structure due to the secondary mirror supports (unchanged from the previous issue);

• a technical note (SPIRE Beam Model Release Note, version 1.0a) providing detailed information on the beam maps and parameters and how they were derived

Empirical beam maps

The empirical beam products consist of two sets of three beam maps, one for each photometer band. The product is derived from scan-map data of Neptune, performed using a custom “fine-scan” observing mode with the nominal source brightness setting. In these fine-scan observations, each bolometer is scanned over Neptune in four different directions. The data were reduced using the standard HIPE scan-map pipeline and the naïve map-maker. Each map constitutes an averaging in the map over all of the individual bolometers crossing the source, and represents the realistic point source response function of the system, including all scanning artefacts. It is worth noting that in a normal SPIRE scan-map, any individual source in the map will be covered by only a subset of bolometers, leading to low-level beam profile variations, from position to position in the map, about the average profile presented here. These beam products also represent the measurement of a source with a ν² spectral shape. A source with a different spectral shape will produce a slightly different beam parameters.

The beam maps for all three bands are displayed in log scaling in Figure 5.8. Four individual maps, one from each of the four observations from which the final beam products are derived, are also available should the user want to investigate the beam stability. The beam product maps are ~ 10 × 30 arcmin in scale and include the same extensions and header information as the nominal maps output from HIPE. There are two versions of each map, one high resolution with a 1 arcsec pixel scale, and another with the nominal SPIRE output map pixel scale of (6, 10, 14) arcsec per pixel for (250, 350, 500) μm. The data have also been normalised to give a peak flux of unity in all three bands.

Figure 5.8: Log scale images for the empirical SPIRE beam model at 250, 350, and 500 μm from left to right respectively. The top row uses a 1 arcsec pixel scale for all maps, and the bottom row uses the nominal SPIRE map pixel scales of 6, 10, and 14 arcsec from left to right respectively.

Note that the ellipticity seen in the maps is not a function of scanning direction, but is constant with position angle. When using these beam models it is advised that the user rotates the beam map so that it matches the position angle of the user’s data. The position angle of HIPE maps can be found in the primary FITS header and is specified by the POSANGLE keyword.

Table 4.1 summarises the beam properties. The main beams are approximated by Gaussian profiles with the nominal FWHM values of (18.2, 24.9, 36.3) arcsec, but explicit integration under the measured beams (see Table 5.2) produces beam areas which are larger, by factors of approximately (1.35, 1.31, 1.27) at (250, 350, 500) μm, than those derived from the main-beam Gaussian approximations due to the low-level sidelobes. It is recommended to use the as-measured beam area in the flux-density to surface brightness conversion.

Beam parameters as a function of pixel size

The basic beam parameters vary as a function of pixel scale, with the FWHM values and beam areas increasing with pixel size. This is expected since the fidelity of the surface brightness reconstruction becomes less reliable at low resolution, particularly with respect to the Airy ring pattern at higher radii from the source peak.

Table 5.2 summarises the basic beam parameters for data binned into 1 arcsec map pixels and for the nominal SPIRE Level-2 map pixel sizes of (6, 10, 14) arcsec at (250, 350, 500) μm. The FWHM values are determined by fitting an asymmetric 2-D Gaussian to the beam maps, and the beam areas are computed by integrating explicitly under the measured beam profiles. Note that the geometric mean FWHM values for the 1 arcsec pixel scale are somewhat smaller than the values previously quoted in v2.1 of this document and in Griffin et al. (2010): (18.1, 25.2, 36.6) arcsec for (250, 350, 500) μm, which were more applicable to the nominal SPIRE Level-2 pixel scales.

Table 5.2: Basic 2-D Gaussian parameters for measured beams with a 1 arcsec pixel size and for the nominal SPIRE Level-2 map pixel sizes (6, 10, 14) arcsec. Uncertainties in the beam FWHM values and areas are estimated at < 1%.

Figure 5.9 shows the variation in beam area, and major and minor FWHM parameters from top to bottom respectively, as a function of map pixel scale. The variation is given for the 250, 350 and 500 μm bands from left to right. The data are fit with a second order polynomial, and the derived fit is displayed on each plot.

Figure 5.9: Variation in beam area, and major and minor FWHM parameters from top to bottom respectively, as a function of map pixel scale. The variation is given for all three bands from 250 to 500 μm from left to right. Second-order polynomial fits to the data are shown by the solid lines, and the derived fits are displayed on each plot.

Raw empirical data

This product is the raw data set from which the empirical beam maps were derived. It has been made available so that users who wish to apply a custom data processing steps can also apply this processing to the beam model data, thereby obtaining a model representative of the beam within their reduced maps.

Optical model of photometer beams

The theoretical model of the beams is based on an optical model of the telescope and the instrument, which has been shown by analysis of in-flight data to provide a highly representative characterisation of the low-level structure in the beams. The model is based on computations of the response function of the end-to-end optical train of the Herschel observatory and SPIRE photometer at individual in-band wavelengths, then summing the monochromatic response with specific weights. The model contains the reconstructed wave-front error distribution of the telescope taken from ground measurements, taking into account the dominant impact of the flight environmental conditions (gravity release, cryo-vacuum operation), as well as the detailed pupil obscuration from the full observatory geometry. The full SPIRE instrument optical model including the entire photometer train up to focal plane is also implemented (see Figure 5.10). The simulated source is a coherent point source with continuum Rayleigh-Jeans (RJ) spectrum, representative of most bright point sources with brightness temperature. The effect of the detector feedhorn is taken into account by including further pupil apodisation with a spectrally-varying edge taper (and associated spectral shift of the diffraction focus) within each band, which has been characterised during SPIRE ground calibration.

Figure 5.10: View of the model geometry (left) and reconstructed telescope pupil optical path difference map from environmental ground measurements by Herschel Observatory industrial contractors (right).

The full band response is obtained by spectral weighting of the set of individual responses. The weights are obtained by product of the Rayleigh-Jeans source spectrum with the instrument Relative Spectral Response Function (RSRF) in each band, the spectral in-band throughput AΩ and finally the spectral in-band coupling, all derived from flight model instrument level ground calibration.

The derived beam models can be considered as “static” noise-free point source reference maps, complementary to the empirical maps which, being flight measured and pipeline generated, include the additional effects among others of electronics detection, scanning, processing and map reconstruction and general additional background noise from sky and observatory.

Figure 5.11 shows the theoretical beam models, all given at a 0.6 arcsec sampling over a 6 × 6 arcmin angular extent and in the spacecraft coordinate system (Y/Z; rotation via the user’s defined position angle will transfer into the relevant sky coordinate systems).

Figure 5.11: Theoretical photometer beams for 250, 350, and 500 μm (left, centre, and right, respectively), with linear scaling (top row) and logarithmic scaling (bottom row)

The model beam product provides significantly higher detail at greater radius but presently is released only at 6 × 6 arcmin scale. Larger scale beam models (e.g., up to 1 deg scale) at lower sampling (e.g. standard 6, 10, 14 arcsec) have been generated in order to provide better estimates on integrated beam extent/effective surface area and may be released later.

5.2.8 Computed conversion factors for SPIRE

Factor K₄ to convert RSRF-weighted flux density to monochromatic flux density

For the standard spectral index of α_S0 = -1 adopted for Herschel, the values of K₄ (as computed using equations 5.17 and 5.18) for the three SPIRE bands are:

Point source (no RSRF weighting):
K_4P (250, 350, 500) μm = (1.0113, 1.0087, 1.0065).

Extended source (λ² RSRF weighting):
K_4E (250, 350, 500) μm = (0.9939, 0.9920, 0.9773).

The conversion factors from point source calibration (SPIRE pipeline convention) to extended source calibration are thus:
K_4E∕K_4P (250, 350, 500) μm = (0.9828, 0.9834, 0.9710).

Level-1 or Level-2 (see Chapter 6) data must be multiplied by these values to convert from point source to extended source calibration.

Note that at the time of writing the latest version of the SPIRE Calibration Tree is v6.1. If one is using data processed with v5.0, then there is no immediate need to re-run the pipeline. A simple multiplicative factor of 1.0067 can be applied to the PMW pipeline output to achieve an equivalent calibration to v6.1.

Factor K_C for colour correction

The colour correction parameter K_C has been computed for various values of α_Snew and the results, following equation (5.20), are shown in Figure 5.12 and Table 5.3.

Table 5.3: Colour correction factor K_C (with α_S0 = -1) as a function of assumed source spectral index. Columns (2, 3, 4) give the values for (250, 350, 500) μm for a point source; columns (5, 6, 7) give the values for (250, 350, 500) μm for an extended source.

Figure 5.12: Colour correction parameter K_C (with α_S0 = -1) vs. assumed source spectral index for point source (top) and extended source (bottom) observations.

These standard colour corrections are recommended to observers. Users wishing to make more refined corrections based on a more complex model of the source spectrum within the band can derive their own corrections using the detailed RSRF, which is also available as a calibration product.

Note that it is the combination of K₄ and K_C that determines how an RSRF-weighted measured flux density is converted to a monochromatic value corresponding to a particular source spectral index. For example, in the case of a spectral index of +3 (typical ν³ dust source), we have:

So, for the same measured signal, the extended source calibration is approximately (5, 5, 9)% higher than the point source calibration at (250, 350, 500) μm.

5.2.9 Conversion from point source to extended source calibration

It is important to note that, since the SPIRE photometer flux calibration is performed on the timeline data, the beam areas equivalent to the beams of the timeline data must be used when calibrating extended emission in terms of surface brightness (Jy/pixel or /sr). This means that the beam areas corresponding to the 1 arcsec pixel scale in Table 5.2 should be used when converting from Jy/beam to Jy/pixel.

For the purposes of point source extraction, beam fitting etc., where the absolute scale of the beam model is unimportant, the appropriate FWHM for a map with a given pixel scale should be used.

The key steps in calibration of extended source emission are illustrated by the following example:

• An extended dust source has a ν³ spectrum and a true brightness of 100 MJy/sr at 250 μm (1200 GHz).

• Its actual monochromatic intensities at (250, 350, 500) μm are therefore (100.0, 36.44, 12.50) MJy/sr

• The corresponding in-beam monochromatic flux densities are these values multiplied by the beam areas:
  (100.0,36.44,12.50) × 10⁶ × (0.9942,1.765,3.730) × 10^-8 = (0.9942,0.6433,0.4663) Jy/beam (this is what we are trying to measure)

• The corresponding in-beam RSRF-weighted flux densities, obtained by integrating the true source spectrum across the passbands using the extended source RSRFs, are (1.0284, 0.6603, 0.4753) Jy/beam

• But the pipeline is based on point source calibration and returns these values multiplied by K_4P :
  (1.0113,1.0087,1.0065) × (1.0284,0.6603,0.4753) = (1.0400,0.6661,0.4785) Jy/beam.
  Note that compared to the true monochromatic flux densities, these values are too high by (4.6, 3.5, 2.6)%.

• Knowing that the source is extended, the user multiplies the pipeline products by K_4E∕K_4P :
  (1.0400,0.6661,0.4785) × (0.9828,0.9834,0.9710) = (1.0221,0.6550,0.4646) Jy/beam
  Note that these values are rather more accurate – high by only (+2.8, +1.8, -0.4)% with respect to the true monochromatic flux densities, but are still based on an assumed ν^-1 spectrum.

• Knowing also that the source has a ν³ spectrum, not ν^-1 as assumed in the pipeline, the user applies the appropriate extended source colour correction factors from Table 5.3 to obtain the true in-beam monochromatic flux densities:
  (0.9727,0.9821,1.0037) × (1.0221,0.6550,0.4646) = (0.9942,0.6433,0.4663) Jy/beam

• What if, inappropriately, the point source calibration is left unchanged and the point source colour correction applied?
  (0.9070,0.9180,0.8952) × (1.0400,0.6661,0.4785) = (0.9433,0.6115,0.4283) Jy/beam
  i.e., the resulting flux densities are too low by (5.2, 5.4, 8.9)% at (250, 350, 500) μm.

5.2.10 Photometer calibration accuracy

SPIRE photometer observations are subject to several kinds of uncertainty.

Absolute calibration uncertainty: This component is associated with our knowledge of the brightness of the primary calibrator, Neptune, and is estimated at ±5%. It is correlated across the three bands, i.e., flux densities in the three bands will move up or down systematically in the event of this calibration being revised.

Relative calibration uncertainty: This uncertainty arises from the process of comparing a source observation with Neptune (using the Neptune-derived voltage to flux density parameters that are implemented in the pipeline). This is a random contribution and has been estimated by careful analysis of repeated measurements of a bright source (actually Neptune itself). The results show that this component is less than 2% in all bands.

At present, we recommend that the overall calibration uncertainty for the SPIRE photometer, taking these two contributions into account, should be taken conservatively as ±7% (the direct rather than quadrature sum of the absolute and relative calibration uncertainties). It should be noted that this is dominated by the absolute component and is thus largely correlated across the three bands.

Photometric uncertainty: This component is due to the source measurement errors. The photometer pipeline produces timelines representing the the in-beam flux density, and some random detector noise will be present in the timelines. Any astrometric errors will also introduce additional noise when timelines are combined in mapmaking. In addition, in order to derive estimates of, for example, the flux density of a point or compact source, users will need to employ some suitable fitting or aperture photometry technique, and additional uncertainties can be introduced due to confusion or source crowding. In addition, slight differences in the choice of pipeline parameters (e.g., for the deglitching and baseline subtraction modules) may produce slightly different results (at the level of a few percent).

It is important to note that these photometric uncertainties will be significant or dominant except for sources which stand out very clearly above any confusion noise or local sky background fluctuations (in which case the calibration uncertainties described above will become significant or dominant). Assessment of the photometric uncertainties will depend on the particular sky brightness distribution and on the source extraction or background subtraction methods, and is is therefore something to be done carefully by the user.

See Section 5.2.11 for some additional considerations relating to the process of point source extraction.

5.2.11 A note on point source extraction from SPIRE Level-2 maps

The SPIRE flux calibration is time-line based (Jy in beam). As a result, the signal level in a map pixel depends on how the square map pixel size compares to the size of the beam. Only in the limit of infinitely small map pixels would a pixel co-aligned with a point source register the true source flux density. It is important to note that no pixel size correction factors are incorporated in the SPIRE Level-2 map-making. For a given map pixel, the flux density value represents the average in-beam flux density measured by the detectors while pointed within that area. Taking the pixel value for the flux density of an isolated co-aligned point source in an otherwise blank map would thus yield an underestimate of the true flux density.

The necessary correction factor is a function of the map pixel size and the beam size, and is a simple multiplicative factor. For a symmetrical Gaussian beam of FWHM θ_Beam, a square pixel of side θ_Pix, and a co-aligned source, the correction factor is:

where erf is the error function erf(x) = ∫ ₀^xe^-t2 dt.

However, in the general case the source will be randomly aligned with respect to the map pixel resulting in a slightly different correction, and a small random uncertainty corresponding to the actual offset of the source with respect to the pixel centre for a particular observation. Moreover, the source is not completely covered on infinitesimal scales; the beams are only sampled along the locations where the detectors crossed over the beam.

Tests of how the measured flux density of point sources in map data have been performed using standard large and small scan map observations of Neptune (for 500 μm only) and γ Dra (for all three bands) to test the pixelisation corrections given by Equation 5.24. Maps from these data were generated at various pixel scales, the data were fitted with Gaussian functions, and then the resulting median flux densities (in the case of the γ Dra data) or median measured/model flux density ratios (in the case of Neptune) were examined to understand how the measured flux densities vary as a function of pixel size.

For 250 μm data, these tests demonstrated that Equation 5.24 provides an accurate correction for point source flux densities measured by PSF fitting in maps in all situations. For 350 μm data, these tests demonstrated that Equation 5.24 provides an accurate correction for point source flux densities measured by PSF fitting in maps for only sources at the centres of small scan maps. The results from the 350 μm large scan map data indicate that the measured flux densities may be lower (by a few percent) than what is implied by Equation 5.24 if the source is not centered within scan legs, although the exact decrease in flux density depends on the location of the source relative to the scan legs. For 500 μm, we found that Equation 5.24 did not provide an accurate correction. Instead, we found that the correction could be corrected using the following empirical equation:

where θ_Pix is the pixel size in arcseconds.

Performing the pixelisation correction introduces an additional uncertainty which is best to determine empirically. At this time, this has only been characterized for 500 μm. The fractional uncertainty due to the pixelisation correction is given by

The default HIPE pixel sizes for (250, 350, 500) μm are θ_Pix = (6,10,14) arcsec. The corresponding pixel size correction factors, given by Equations 5.24 and 5.25, are P = (0.951,0.931,0.902). From Equation 5.25, the corresponding percentage uncertainties introduced into the point source flux density estimation at 500 μm is 1.5%. This uncertainty should be added in quadrature to the other statistical uncertainties of the measurement. Note that similar uncertainties may be appropriate to apply to 250 and 350 μm data but have not yet been derived.

The following approach will yield the correct flux density of an isolated point source in an otherwise blank map:

1. Associate each map pixel flux density value with the central position of the pixel.

2. Derive the map pixel flux density that would have been recorded had the source been co-aligned with a pixel centre. This can be done by fitting the appropriate function to these data points and deriving the peak value. This function to be fitted is the beam profile convolved with the map pixel size. If the true beam profile were a 2-D Gaussian, the constrained parameters of this function would be (major axis, minor axis, position angle) and the free parameters would be (peak value, position of peak value).

3. Divide the resulting peak value by the pixelisation correction factor P.

5.2.12 Summary

The photometer pipeline produces monochromatic in-beam flux densities at 250, 350 and 500 μm, calculated under the assumptions of (i) a point source observation and (ii) a flat νS_ν spectrum.

To convert the pipeline output from point source to extended source calibration, the flux densities should be multiplied by (K_4E∕K_4P ) = (0.9828, 0.9839, 0.9710) for (250, 350, 500) μm.

For extended sources, the surface brightness can be obtained from the flux density in Jy/beam by dividing it by the measured beam area.

To convert the pipeline flux densities to an assumed source spectral index other than α_S = -1, they should be multiplied by the appropriate factors from Table 5.3 (which are different for point source and extended sources). For the same measured signal, the extended source calibration is typically 5% higher than the point source calibration.

Current flux calibration accuracy is estimated conservatively at ± 7%, dominated by the 5% absolute uncertainty in the Neptune model, and largely correlated across the bands.

For highest accuracy in the extraction of point source flux density from a map, careful attention must be paid to the effect of finite map pixel size on peak flux density, and a pixelisation correction uncertainty is introduced into the flux density estimate.

5.2.13 Future plans for photometer flux calibration

SPIRE flux calibration is now in the regime of sub-10% accuracy for point sources and ~ 10-15% for extended emission. A Herschel calibration workshop in December 2010 reviewed various aspects of flux calibration including: (i) the accuracy and compatibility of the Neptune-based calibration (used by SPIRE) and the stellar-based calibration (used by PACS); and (ii) the methods, assumptions and conventions used by both SPIRE and PACS. The results showed that the Neptune-based calibration scheme adopted by SPIRE and the stellar-based scheme adopted by PACS are consistent to within better than 5%. Further refinements to the calibration scheme presented here may be made in the future based on (i) revision of the basic Neptune brightness model used, and/or (ii) a more detailed treatment of the extended source calibration, which is currently in development, involving a more precise method of accounting for the variation of the beam profile across the bands. We expect any such updates to produce a new calibration consistent with the current one, but with smaller uncertainties.

5.3 Spectrometer flux calibration

The calibration of the spectrometer follows a different method to that adopted for the photometer. The FTS detector output is not a direct measurement of the flux density integrated over the passband as in the photometer, but depends on the Fourier components of the spectral content. Therefore Equation (5.12) is not directly applicable but an analogous equation can be used to correct for any non-linearity between absorbed power and bolometer voltage before transforming into the frequency domain. The parameters in this scheme are derived from a thermal model of the bolometer response to absorbed power. Once a linearised voltage timeline has been obtained, the signal versus optical path difference is calculated using the spectrometer mechanism position and corrections for phase error in forward and backward scans due to the time response of the bolometers and electrical filters are made (see Fulton et al. 2008). At this stage the timeline is referred to as an interferogram (linearised voltage vs. optical path difference).

The next step is to subtract the baseline of the interferogram and apply further phase correction. An apodization function can be applied if desired. The final interferogram is then transformed into the spectral domain. The spectrometer bolometers receive radiation from the combination of the astronomical source, the telescope, and the instrument itself. It is therefore necessary to subtract the excess emission to recover the source spectrum. This is done using the following model:

where R_Source, R_Tel, and R_Inst are the RSRFs applicable to the source, telescope and instrument contributions, and B_Source, B_Tel and B_Inst are the corresponding intensities (in the case of the instrument, B_Inst is due to the thermal emission from within the ~ 5-K FPU enclosure).

The emission from the telescope is determined using its emissivity (Fischer et al., 2004):

where λ is the wavelength in μm. The final emission from the telescope, assuming that there is no stray light, and taking account of emission from both the primary and secondary mirrors, and reflection from the secondary, is taken to be

where B(T,ν) is the Planck function, expressed in terms of frequency so that the final units can be easily converted to Jy:

The temperatures of the telescope primary and secondary mirrors, T_M1 and T_M2, are measured by thermistors on the spacecraft and are available as auxiliary products in the observation context.

The emission due to the internal temperature of the instrument is calculated using FPU thermistors which measure the instrument baseplate temperature, T_Inst,

The final source spectrum is obtained from:

where V _Obs is the observed spectrum in units of V/cm^-1. The telescope and instrument RSRFs are derived from observations of a dark region of the sky made throughout the mission and stored as calibration files. The RSRF applicable to the source is derived from the telescope RSRF for uniformly extended emission, with units of (V cm/(W m^-2 Hz^-1 sr^-1)). Data calibrated with the extended correction can easily be converted to MJy sr^-1 by multiplying by 10²⁰. Figure 5.13 shows these extended source RSRFs for the two FTS bands.

Figure 5.13: The telescope high resolution, unapodized and with nominal bias settings RSRF (R_Tel) for the two FTS bands. There are slight differences in the telescope RSRF for forward and reverse scans: forward scans for SSW and SLW are shown in cyan and orange respectively, the reverse scans RSRFs are shown in blue (SSW) and red (SLW).

A correction related to the spectrometer beam shape (see next section) is required to convert from the extended calibration to a point source calibration for the central detector pair. It should also be noted that channel fringes and spectral features in the passband of the instrument will change as a function of source extent.

The point source conversion factor is determined from observations of Uranus. The Uranus model is as described in  5.1.2. Equations 5.34 and 5.35 in the next section define the point source RSRF, and the correction factor needed to convert from extended to point source calibrated data. The extended source calibration has been tested against the planet models using knowledge of the spectrometer beam shape and source coupling efficiencies and found to give very good results (see Swinyard et al. 2010).

5.3.1 Spectrometer beam properties

The FTS beam size as a function of frequency has been measured directly by taking medium resolution spectra on a point source (Neptune) placed at different locations with respect to the central detectors (SSWD4/SLWC3) by stepping the telescope pointing. The beam shows a highly structured behaviour in the variation in beam size with frequency (Swinyard et al., 2010). This is expected from the multi-moded feedhorns used for the spectrometer arrays, as different detector feedhorn/waveguide modes become propagated at certain frequencies in the band (the number of propagated modes increases with frequency).

The central part of the measured beam pattern can be fitted with a 2-D Gaussian or Airy profile, and the results show good agreement between the two with a typical residual ellipticity of 2-5%, and a wavelength dependence with good correspondence to the expected mode onset of the feedhorns (Naylor et al., 2010). However, there is significant power outside the main beam at all frequencies, due to the sidelobes. When analysing extended emission, the units of the pipeline-processed FTS spectra are in surface brightness (W m^-2 Hz^-1 sr^-1), and detailed knowledge of the beam pattern is needed to recover in-beam flux densities.

To calculate the beam area applicable for extended emission, the étendue (the product of effective telescope area and the beam solid angle on the sky, A_effΩ) has been derived from mapping observations of Neptune. In theory, for a single-moded system the étendue at wavelength λ is equal to λ². In practice, the presence of optical aberrations, diffraction, and partial coherence induces significant deviation from the theory. This can be represented by a wavelength-dependent factor, γ (sometimes called M²):

where γ is a dimensionless factor derived from a characteristic beam dimension by taking the ratio of the measured value to the prediction from fundamental mode Gaussian beam theory. For SPIRE, γ has been calculated from the ratio of the measured Neptune and theoretical beam FWHM: γ = FWHM_measured∕FWHM_theory.

In addition, the coupling efficiency of a point source to the beam, η_P , has been derived from the combination of feedhorn modes using the Coherent Mode Representation (Mandel & Wolf, 1995).

The beam area can be extracted from the étendue using knowledge of the effective area of the Herschel telescope as viewed by the SPIRE FTS. This area is influenced by frequency-dependent illumination and diffraction in the instrument optics. It has been determined empirically by comparing the instrument RSRF derived from Uranus and that derived from the telescope background (which provides extended illumination).

The point-source and extended-source RSRFs are defined as follows:

where M_Uranus and M_Telescope are the models of Uranus and the telescope emission respectively (see Chapter 4), ε is the emissivity of each telescope mirror, and V is the measured signal from the detectors.

The ratio of point-like to extended RSRFs is equal to the beam area multiplied by the coupling efficiency for a point source:

The effective telescope area is then given by,

This may also include any additional variations, for example due to vignetting. The result is shown in Figure 5.14 in the form of effective telescope diameter (using A = πD²∕4), with straight line fits to smooth over small scale effects due to differences in the fringing pattern for point-like and extended sources.

Figure 5.14: Effective telescope diameter vs. wavenumber

The straight line fit to the effective telescope area has been used to calculate values for the beam area as a function of wavelength from the étendue. This is provided in HIPE as a calibration file. The beam areas are roughly a factor of 2-3 larger than the Gaussian or Airy fits, reflecting the power picked up in the outer parts and sidelobes of the beam. This effect is very similar to that seen, for instance, in SCUBA maps from the JCMT for which a scaling factor of 0.43 (equivalent to a factor of 2.3 in beam area) is needed to take account of the “error beam” for extended emission at 450 μm (Sandell et al., 2001).

Table 5.4: Variation of beam FWHM and extent across the FTS bands.

Table 5.4 and Figure 5.15 summarise the FWHM variation across the band from Gaussian fits to the beam, and the effective beam solid angle for extended emission. The last column gives the “effective” FWHM – this is calculated from the beam extent as if it were Gaussian distributed. For calculations of source emission from extended objects, only the beam solid angle should be used.

Figure 5.15: Variation of beam FWHM and solid angle across the FTS bands

5.3.2 Extended sources and spectral mapping

Spectral mapping observations are performed using all of the detectors in the spectrometer arrays. In the case of fully sampled (Nyquist sampled) or intermediate sampled (half Nyquist spacing) maps, the resulting data are regridded into a regular spectral cube by the pipeline. The flux density calibration of individual detectors is carried out as described above using the telescope itself as the standard calibrator. Flat fielding across detectors is taken into account by deriving a separate RSRF for each bolometer.

It should be noted that the RSRF derived from the telescope emission is valid for a uniformly extended source that completely fills the detector field of view, and any source morphology would change the calibration.

5.3.3 Dynamic range and interferogram clipping

The dynamic range of the detectors is determined once, at the beginning of each observation, by an algorithm that sets an offset level in the detector electronics as described in Griffin (2008). The level used is determined by the baseline of the interferogram and does not take account of the modulation at zero path difference (the interferogram central maximum). For this reason, the additional thermal source, SCAL, was included in the second port of the FTS with the aim of reducing the modulation, thereby reducing the overall dynamic range requirements on the FTS on-board signal chain. However, interferograms measured on sources as bright as Uranus have shown that, even with the SCAL source off, the signal at the central peak does not saturate, or at most only a few samples are saturated, as long as the detector bias is appropriately set (see Section 5.3.4). It is therefore not necessary to use SCAL to null the telescope emission – a consequence of the lower total emission from the telescope and straylight compared to the expected values used in the initial design of the SPIRE instrument. For this reason, and because operating SCAL adds to the photon noise in the measurement, it has been decided not to use the SCAL source in routine observations. An additional benefit of this mode of operation is that, with SCAL off, all spectral contributions from the instrument, be they from SCAL or other optical components, are limited primarily to the SLW band.

5.3.4 Bright source mode

Very bright targets (e.g. Orion, Sgr B2, Mars) can be observed with the FTS using a bright source mode. This is designed to allow observations of sources which would otherwise saturate the detectors. It can be used with any of the spectrometer AOT combinations.

In the measured interferogram, the total power received is reflected in the amplitude of the modulation at zero path difference (ZPD). This means that once a certain source strength is reached, the amplitude of modulation may exceed the dynamic range and the interferogram can be clipped. Signal clipping can occur either at the maximum or the minimum of the interferogram – it can be corrected if there are only a small number of consecutive clipped samples, but for very bright sources, the clipping can be more severe. In cases where it is impossible to correct for clipped interferograms close to ZPD, the continuum shape and level will be affected across the spectrum. The bright source mode addresses this problem by using a different bias amplitude and phase for the bolometers to lower their responsivity and so reduce the maximum modulation in the interferogram.

For mapping observations in bright mode, the dynamic range of the detectors is set at every jiggle position to maximize the number of interferograms within the dynamic range (for nominal mode, this is only done once at the beginning of the observation).

The advantage in using bright mode is that clipping is significantly reduced (and in most cases should be eliminated for the central detector pair) for sources up to the strength of Mars (~ 15,000 Jy). This means that the absolute level (and shape) of the spectrum can be well calibrated. However, as noted in Section 4.2.4, due to the reduction in responsivity needed for bright mode, the sensitivity is reduced compared to nominal mode by a factors of approximately 2 for the SLW array and 4 for the SSW array.

As clipping occurs only around the peak modulation in the interferogram, spectral lines are relatively unaffected (the information about spectral lines is spread through the interferogram up to large optical path differences).

The bright mode is advantageous for jiggle mapping observations where there are large brightness gradients across the region to be mapped. In nominal mode mapping observations, the absolute and dynamic range of the detector readout is set once, at the beginning of the observation. For regions with large brightness contrast, and/or containing embedded bright sources, this is insufficient to ensure that the optimum readout range is set for every jiggle position. For some jiggle positions, interferograms could be completely out of range – i.e. completely saturated. This problem is avoided in bright mode because the readout range is set separately for every jiggle position. The cost is a slight increase in the overhead time by ~ 25 seconds per jiggle position.

The central detector pair (SSWD4/SLWC3) have been found to show clipping for sources brighter than Uranus (~ 400 Jy at centre of SSW band and ~ 200 Jy at centre of SLW band). This indicates that for sources much brighter than this, the bright mode should be considered in order to obtain the best calibration of the continuum and not lose information through clipping. However, in light of the sensitivity penalty the optimum cutoff in source brightness between nominal and bright modes is somewhat subjective. The pipeline clipping task has been shown to successfully “reconstruct” interferograms with a few consecutive clipped points, and so if the main goal of the observation is the detection of weak lines, it may still be preferable to use the nominal mode above the threshold (albeit with a cost in accuracy of the continuum).

In summary, the recommendations are as follows:

• If the source is less bright than Uranus, use nominal mode.

• If the source is brighter than Uranus but not by too much (a couple of hundred Jy), there may be clipping in nominal mode, but it can be reconstructed in the data reduction – therefore use nominal mode unless it is critical to get the best possible calibration of the absolute continuum shape.

• If the source is much brighter than Uranus (a thousand/thousands of Jy) and a factor of 2-4 loss in sensitivity is not critical, it is best to use bright mode.

• If sensitivity is critical, and accuracy of the continuum is not, nominal mode could be used for sources brighter than Uranus (contact the HSC/ICC for further advice if in doubt).

• For mapping observations of areas containing bright sources, or large brightness gradients, use bright mode.

The bright mode has been successfully used for point sources up to the brightness of Mars (~ 15,000 Jy in SSW). The Orion Bar (max. 600 Jy in-beam in both bands) has been successfully observed using nominal mode, but Orion OMC1 (~ 5,000 Jy) required bright mode (particularly for mapping).

5.3.5 Spectrometer calibration accuracy

SPIRE spectrometer observations are subject to two kinds of uncertainty in an analogous way to the photometer (see Section 5.2). The first is the absolute uncertainty associated with our knowledge of the brightness of the primary calibrator – Uranus in this case. This is estimated at ± 5%, and is correlated across the spectrum. The second component of uncertainty is due to the statistical errors of both the measurements of the source and of the measurements used to derive the RSRF, taking into account all forms of noise (e.g., detector noise, pointing uncertainty and jitter, etc.). This can be regarded as random component.

At present, a conservative overall uncertainty is 15-20% in the SSW band and 20-30% in the SLW band above 20 cm^-1 and up to 50% below 20 cm^-1. The SPIRE ICC is continuing to improve the calibration accuracy, and future developments will be announced via the HSC.

For spectral mapping observations, there is currently an additional uncertainty in the continuum calibration due to imperfect flat fielding between different detectors in the array. This is expected to improve with better characterisation of the array. It leads to an additional uncertainty of 10-15% in the absolute continuum levels in the final gridded spectral cube.

5.3.6 Summary

The spectrometer pipeline produces calibrated spectra from single pointed sparse observations in units of flux density (Jy) calculated under the assumption of a point source observed with the central detector pair (SSWD4/SLWC3).

For spectral mapping observations with full or intermediate spatial sampling, the pipeline produces calibrated, regularly gridded spectral cubes in units of intensity (W m^-2 Hz^-1 sr^-1) under the assumption of a uniformly extended source. Conversion of surface brightness to flux density can be made using the wavelength-dependent beam solid angle.

Current flux calibration accuracy is estimated conservatively at 15-20% in the SSW band and 20-30% in the SLW band above 20 cm^-1 and up to 50% below 20 cm^-1.

Chapter 6
SPIRE data products

In this chapter we briefly describe the data products and the data structure coming from SPIRE observations. A comprehensive explanation, and practical guidelines for accessing the data, running the pipeline and doing quick interactive analysis can be found in the SPIRE Data Reduction Guide and the SPIRE Pipeline Specification Manual. Both of these manuals are contained within the Help documentation inside the Herschel Interactive Processing Environment (HIPE). The manuals are also available on the HSC web pages as standalone documents.1

Astronomer users will receive data that has already been processed through the standard pipelines to several levels. The processing levels of the SPIRE pipeline and user deliverables are outlined in Figure 6.1. In general, Level 0 data corresponds to the raw data, formatted from the raw telemetry by an external pre-processing stage. These Level 0 Data Products are then passed through a processing stage referred to as the Engineering Conversion that creates the Level 0.5 Data Products in a meaningful and manageable form. The SPIRE AOT specific pipelines then process these Level 0.5 Data Products to produce the science usable, calibrated Level 1 Data Products. Further advanced processing to create products such as maps produce the high-level Level 2 Data Products. Quality Control is carried out by the HSC and delivered to the user.

Figure 6.1: The processing levels of the SPIRE pipeline and user deliverables.

The smallest “piece” of SPIRE observational data is called a Building Block. These building blocks correspond to basic operations within an observation and as the name suggests every SPIRE AOT is built up from a combination of these building blocks. Building blocks are usually in the form of Timeline Data Products.

Example building blocks may be:

• A scan line in a map.

• A single 7-point jiggle.

• A set of spectrometer scans.

• A segment of housekeeping scans.

• A motion of the Beam Steering Mirror (BSM).

Building blocks and other products are grouped into a context. A context is a special kind of product linking other products in a coherent description and can be thought of as an inventory or catalogue of products. The SPIRE processed observation consists of many such contexts enclosed within one observation context. Therefore, each set of building blocks have a context. Each processing level in the SPIRE pipeline has a context and the entire observation has a context. Thus a complete observation may be thought of as a big SPIRE onion as depicted in Figure 6.2. Moreover, contexts are not just for building block products and higher processed data products, there are contexts for Calibration Products and contexts for Auxiliary Products (e.g. pointing) and even a context for Quality Control. The entire SPIRE Observational Context is shown in Figure 6.2 for all products from the raw building block data to the final high level processed end products from the pipeline. This is the structure and content that you should receive for your SPIRE observation from the Herschel Science Archive (HSA).

Figure 6.2: The complete Observation Context of a SPIRE observation.

The main aim of the data processing pipeline is to convert the raw data as received form the observatory to high level scientifically meaningful products with all instrumental effect removed. All the processing steps are presented in much greater detail in the above mentioned references. The first step to produce Level-0.5 products is applicable to all SPIRE observing modes. In general it is expected that users will start their interactive processing from this Level-0.5 stage, i.e. the timelines in engineering units. This level is the starting point for AOT specific pipelines which produce the final scientifically meaningful data products with all instrumental effects removed and with calibrated physical units. The “standard” pipelines are run on all executed Herschel observations in the context of the Standard Product Generation (SPG). This is performed by the Herschel Science Centre, and upon successful completion of the pipeline and positive quality control checks, the products are ingested in the Herschel Science Archive (HSA).

Bibliography

   Ade, P. et al., 2006, Proc. SPIE 6275, 62750U

   Audley, D. et al., 2007, in Proc. Exploring the Cosmic Frontier, Astrophysical Instruments for the 21^st Century, Springer-Verlag, p. 45

   Cantalupo C.M., Borrill J.D., Jaffe A.H., Kisner T.S., Stompor R., 2010, ApJS, 187, 212

   Chattopadhaya, G. et al, 2003, IEEE. Trans. Microwave Theory and Techniques, 51, 2139

   Decin, L. & Eriksson, K., 2007, Theoretical Model Atmosphere Spectra Used for the Calibration of Infrared Instruments, A&A, 472, 1041, 2007.

   De Graauw, Th. et al., 2010, The Herschel-Heterodyne Instrument for the Far-Infrared (HIFI), A&A, 518, L6

   Dohlen, K. et al., 2000, Proc. SPIE 4013, 119

   Dowell, D. et al., 2003, Proc. SPIE, 4855, 73

   Duband, L. et al., 1998, Cryogenics, 48, 95

   Fischer, J. et al., 2004, Cryogenic far-infrared laser absorptivity measurements of the Herschel Space Observatory telescope mirror coatings, Applied Optics, 43, 3765

   Fulton, T. et al., 2008, Proc. SPIE, Vol. 7010, 70102T.

   Griffin, M. J., 2008, The SPIRE Analogue Signal Chain and Photometer Detector Data Processing Pipeline, SPIRE-UCF-DOC-002890, Issue 6, November 2008.

   Griffin, M.J. & Orton, G.S., 1993, The Near Millimeter Brightness Temperature Spectra of Uranus and Neptune, Icarus, 105, 537.

   Griffin, M.J. et al., 2002, Applied Optics, 31, 6543

   Griffin, M.J. et al., 2006, Herschel-SPIRE: Design, Performance, and Scientific Capabilities, Proc. of SPIE 6265, 7.

   Griffin, M.J. et al., 2010, The Herschel-SPIRE Instrument and its in-flight performance, A&A, 518, L3

   Hargrave, P. et al., 2006, Proc. SPIE 6275, 627513

   Hartman R.C. et al.1996, Simultaneous Multiwavelength Spectrum and Variability of 3C 279 from 10⁹ to 10²⁴ Hz, ApJ, 461, 698.

   Hildebrand, R. et al., 1985, Far-infrared and Submillimeter Brightness Temperatures of the Giant Planets, Icarus, 64, 64.

   Lebofsky, L.A. et al., 1986 A Refined Standard Thermal Model for Asteroids Based on Observations of 1 Ceres and 2 Pallas, Icarus, 68, 239

   Lindal, G.F., et al., 1987, The Atmosphere of Uranus: Results of Radio Occultation Measurements with Voyager 2, J. Geophys. Res., 92, 14987.

   Lindal, G., 1992, The Atmosphere of Neptune: an Analysis of Radio Occultation Data Acquired with Voyager 2, Astron. J., 103, 967.

   Mandel, L. & Wolf, E., 1995, Optical coherence and quantum optics, CUP

   Mather, J.C., 1982, Bolometer noise: nonequilibrium theory, Applied Optics 21, 1125.

   Marth, A., 1897, On the Apparent Disc and on the Shadow of an Ellipsoid, MNRAS, 57, 442.

   Moreno, R., 1998 PhD Thesis, Université Paris VI.

   Moreno, R., Neptune and Uranus planetary brightness temperature tabulation, available from ESA Herschel Science Centre ftp://ftp.sciops.esa.int/pub/hsc-calibration, 2010

   Müller, Th. & Lagerros, J.S.V., 2002, Asteroids as Calibration Standards in the Thermal Infrared for Space Observatories, A&A, 381, 324.

   Müller, Th, 2009, Asteroid Calibration Quality Information for COP and Early PV, 8 May 2009, Asteroid_quality_TM_08052009.pdf (available from ESA Herschel Science Centre)

   Naylor, D. & Tahic, K., 2007, J. Opt. Soc. Am. A. 24, 3644

   Naylor, D. et al., 2010, In-orbit performance of the Herschel/SPIRE imaging Fourier transform spectrometer, SPIE, 7731, 29

   Nguyen, H., et al., 2010, A&A, 518, L5

   Orton, G.S., et al., 1986, Submillimeter and Millimeter Observations of Uranus and Neptune, Icarus, 67, 289.

   Pilbratt, G. et al., 2010, Herschel Space Observatory – An ESA facility for far-infrared and submillimeter astronomy, A&A, 518, L1

   Pisano, G. et al., 2005, Applied Optics IP, 44, 3208

   Poglitch, A. et al., 2010, The Photodetector Array Camera and Spectrometer (PACS) on the Herschel Space Observatory, A&A, 518, L2

   Rownd, B. et al., 2003, Design and performance of feedhorn-coupled arrays coupled to submillimeter bolometers for the SPIRE instrument aboard the Herschel Space Observatory, Proc. SPIE 4855, 510.

   Sandell, G., Jessop, N., and Jenness, 2001, T SCUBA Map Reduction Cookbook, http://www.starlink.rl.ac.uk/star/docs/sc11.htx/sc11.html

   Sudiwala, R.V, Griffin, M.J. and Woodcraft, A.L., 2002, Thermal modelling and characterisation of semiconductor bolometers, Int. Journal of Infrared and mm Waves, 23, 545.

   Swinyard, B. et al., 2003, Proc. SPIE 4850, 698

   Swinyard, B. M. et al., 2010, In-flight calibration of the Herschel-SPIRE instrument, A&A, 518, L4

   Turner, A.D. et al., 2001, Si₃N₄ micromesh bolometer array for sub-millimeter astrophysics, Applied Optics 40, 4921.

   Ulich, B.L. & Haas, R.W., 1976, Absolute Calibration of Millimeter-Wavelength Spectral Lines, ApJS, 30, 247.