Like most other heterodyne instruments, HIFI makes use of the two internal loads to provide the bandpass calibration (sensitivity) for each backend (spectrometer) channel and polarization. The effective radiation offered by these loads is corrected from the imperfect coupling of the mixer beam to the load apertures. These couplings were measured on the ground during instrument level testing. The instrument bandpass γ_rec and the receiver temperature J_rec obtained via the load measurements are provided by Eq. (9) and (10) from [10].

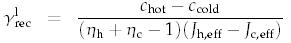
The "l" superscript indicates that the bandpass and receiver temperatures are measured on the internal loads.

In the above equations c indicates count rates measured on hot or cold loads, z a "zero frame" removal. J's indicate the hot and cold load effective temperature measures -- as measured by temperature sensors on the internal hot and cold loads, and η_h and η_c indicate the coupling of the beam to the hot and cold loads.

At this stage of our calibration, we have made the following assumptions:

In addition to the two internal load calibrations, HIFI will use the observation of blank sky to reveal additional calibration information on the system. In contrast to ground-based observations where the observation of a reference position free of emission would provide mainly information about the atmosphere, we can use such a measurement for a better characterisation of the instrument response itself. In particular, measurements on blank sky help in deriving information about the difference in standing wave patterns that are occur between the load measurement and the astronomical observation.

The idea behind this OFF measurement is that the full frequency resolution of HIFI is not necessary to sufficiently sample the standing waves to be corrected in the system. Considering the typical optical paths involved in the instrument, it is sufficient to measure the standing wave effect with a frequency resolution of 10 MHz. Since we are smoothing our OFF measurements to a lower resolution some reduction in the observing time is required for characterisation of the standing waves with sufficient signal-to-noise.

For an accurate treatment of the standing wave effect, additional assumptions must be made on how they contribute to the instrument response (standing wave model). Two other parameters add to the unknowns when considering OFF measurements: the telescope forward efficiency η_l, and the telescope radiation J_R,eff. All these effects are superposed in the OFF measurements. It is however reasonable to assume that standing waves will appear as the variation across a band while the telescope contribution will be identified as an average contribution over the band (see [10]).

So far we have considered three standing wave cases:

The preference to one or other of these models is currently being investigated for different LO settings and cases from the performance verification phase.

To correct for instrument drift effects, the astronomical observations will use a differencing scheme where the astronomical source and a reference are observed in an alternating sequence. HIFI uses four basic approaches: total power (also called Position Switch), sky chop (also called Double Beam Switch), load chop and frequency switch (see chapter on observing modes). Reference [10] gives some examples of the equations obtained in various differencing schemes, and depending on the standing wave model approach. In particular, it shows how both line and continuum contributions to the signal can be separately treated. The continuum term only contains the radiation from the source and the blank sky in its surrounding. The continuum radiation seen from the warm telescope structure cancels out in all equations by means of the OFF calibration.

In essence, the OFF calibration combined to the differencing approach always provides a double difference. The double difference corrects for the standing waves in the baselines but from the point of view of observational noise, ON and OFF measurements are equivalent. Thus the use of an OFF calibration may be less efficient that total power measurements. This is depending on the system stability, which could offer the possibility to use one OFF calibration measurement for a series of source measurement.

In all equations and references mentioned above, it has been assumed that the instrument response to any radiation field is linear. Deviations from a linear behaviour are expected mainly in the IF branch including the spectrometers. However from ground-based measurements, it was concluded that these deviations are not significant (1% or less), and can in any case be measured and corrected in the data processing.

The main contribution from the blank sky comes from the dust emission in the Milky Way, which is the brightest extended source of radiation in the considered wavelength region. For a typical Galactic OFF position 4-5 degrees from the Galactic plane at 500 GHz, the continuum intensity corresponds to 10^-3 K, and thus is far from having any noticeable influence. In sky regions closer to the Galactic plane, the continuum intensity increases but remains insignificant. Only in the direction of the Galactic centre the continuum emission becomes no longer negligible. These numbers are based on the work of Schlegel et al. ([15]) who obtained the spatial distribution of the dusty density and temperature combining IRAS and DIRBE data.

The HIFI calibrated product, as obtained from the pipeline, is provided in antenna temperature (T_A). To convert this to a source flux in Janskys requires some knowledge of the beam at the frequency used. HIFI beam information is discussed in Section 5.5.2, “Beam Characteristics”. The formula for conversion is:

S/T_A = 326.9/η_A Jy/K

The value of η_A for each subband is listed in Table 5.5, “HIFI beam efficiencies ”.